题目内容
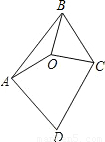
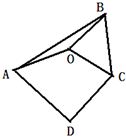 11、如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是
11、如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是150
度.分析:首先由OA=OB=OC,得出∠OAB+∠OBA+∠OBC+∠OCB=140°,进而由四边形内角和定理得出,∠OAB+∠ABC+∠OCB=140°,再利用四边形内角和从而可得出答案.
解答: 解法1:∵OA=OB=OC,
解法1:∵OA=OB=OC,
∴∠OAB=∠OBA,∠OBC=∠OCB,
∵∠ABC=∠OBA+∠OBC=70°,
∴∠OAB+∠OBA+∠OBC+∠OCB=140°,即∠OAB+∠ABC+∠OCB=140°,
又∵∠ABC+∠BCD+∠ADC+∠BAD=360°,即∠ABC+∠OCB+∠OCD+∠ADC+∠DAO+∠OAB=360°,∵∠ADC=70°,∠OAB+∠ABC+∠OCB=140°,
∴∠DAO+∠DCO=360°-140°-70°=150°.
解法2:由AO=BO=CO,可知O是三角形ABC的外心,
∠ABC是圆周角,∠AOC是圆心角,
所以∠AOC=2∠ABC=140°,
又∠D=70°,
所以∠DAO+∠DCO=360°-140°-70°=150°.
答案为:150.
 解法1:∵OA=OB=OC,
解法1:∵OA=OB=OC,∴∠OAB=∠OBA,∠OBC=∠OCB,
∵∠ABC=∠OBA+∠OBC=70°,
∴∠OAB+∠OBA+∠OBC+∠OCB=140°,即∠OAB+∠ABC+∠OCB=140°,
又∵∠ABC+∠BCD+∠ADC+∠BAD=360°,即∠ABC+∠OCB+∠OCD+∠ADC+∠DAO+∠OAB=360°,∵∠ADC=70°,∠OAB+∠ABC+∠OCB=140°,
∴∠DAO+∠DCO=360°-140°-70°=150°.
解法2:由AO=BO=CO,可知O是三角形ABC的外心,
∠ABC是圆周角,∠AOC是圆心角,
所以∠AOC=2∠ABC=140°,
又∠D=70°,
所以∠DAO+∠DCO=360°-140°-70°=150°.
答案为:150.
点评:此题主要考查了多边形内角和定理,以及等腰三角形的性质,解决问题的关键是得出∠OAB+∠ABC+∠OCB=140°,进而求出∠OAB+∠ABC+∠OCB=140°是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 5、如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
5、如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )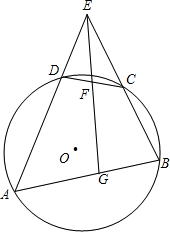 如图,已知⊙O是四边形ABCD的外接圆,直线AD,BC相交于点E,F是弦CD的中点,直线EF交弦AB于点G,求证:
如图,已知⊙O是四边形ABCD的外接圆,直线AD,BC相交于点E,F是弦CD的中点,直线EF交弦AB于点G,求证: 6、如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=65°,则∠DAO+∠DCO的度数是( )
6、如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=65°,则∠DAO+∠DCO的度数是( )