��Ŀ����
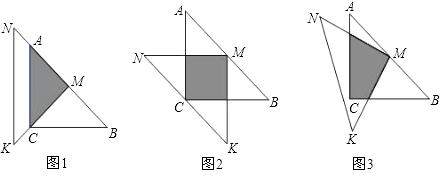
����Ŀ����ͼ������Rt��ABC�У���ACB=90�㣬AC=BC=1����AC����ֱ��a�ϣ�����ABC�Ƶ�A˳ʱ����ת��λ�âٿɵõ���P1 �� ��ʱAP1= ![]() ����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڿɵõ���P2 �� ��ʱAP2=
����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڿɵõ���P2 �� ��ʱAP2= ![]() +1����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۿɵõ���P3ʱ��AP3=
+1����λ�âڵ��������Ƶ�P2˳ʱ����ת��λ�âۿɵõ���P3ʱ��AP3= ![]() +2�����˹��ɼ�����ת��ֱ���õ���P2026Ϊֹ����AP2016= ��
+2�����˹��ɼ�����ת��ֱ���õ���P2026Ϊֹ����AP2016= �� 
���𰸡�1344+672 ![]()
���������⣺AP1= ![]() ��AP2=1+
��AP2=1+ ![]() ��AP3=2+
��AP3=2+ ![]() ��
��
AP4=2+2 ![]() ��AP5=3+2
��AP5=3+2 ![]() ��AP6=4+2
��AP6=4+2 ![]() ��
��
AP7=4+3 ![]() ��AP8=5+3
��AP8=5+3 ![]() ��AP9=6+3
��AP9=6+3 ![]() ��
��
��2016=3��672��
��AP2013=��2013��671��+671 ![]() =1342+671
=1342+671 ![]() ��
��
��AP2014=1342+671 ![]() +
+ ![]() =1342+672
=1342+672 ![]() ��
��
��AP2015=1342+672 ![]() +1=1343+672
+1=1343+672 ![]() ��
��
��AP2016=1343+672 ![]() +1=1344+672
+1=1344+672 ![]() ��
��
�ʴ�Ϊ��1344+672 ![]() ��
��
�ɵ���ֱ�������ε����ʺ���֪�����ó�AP1= ![]() ��AP2=1+
��AP2=1+ ![]() ��AP3=2+
��AP3=2+ ![]() ��AP4=2+2
��AP4=2+2 ![]() ��AP5=3+2
��AP5=3+2 ![]() ��AP6=4+2
��AP6=4+2 ![]() ��AP7=4+3
��AP7=4+3 ![]() ��AP8=5+3
��AP8=5+3 ![]() ��AP9=6+3
��AP9=6+3 ![]() ��ÿ����һ�飬����2013=3��671���ó�AP2013 �� ���ɵó������
��ÿ����һ�飬����2013=3��671���ó�AP2013 �� ���ɵó������

��ϰ��ϵ�д�
 �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
�����Ŀ