Question

边长为2的正方形的顶点A到其内切圆周上的最远距离是________，最短距离是________．

Answer 1

+1    -1
分析：根据题意画出图形，由正方形的性质可知，正方形的对角线AC必过⊙O的圆心，故顶点A到其内切圆周上的最远距离为AF，最短距离是AE，过O作OG⊥AG，由正方形的性质可求出OA及OG的长，进而可求出顶点A到其内切圆周上的最远距离与最短距离．
解答：解：如图所示，过O作OG⊥AG，
∵AD=2，
∴AG=OG=1，
∴OA===，
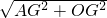∴AE=OA-OE=-1，AF=OA+OF=+1，
∴顶点A到其内切圆周上的最远距离是+1，最短距离是-1．
故答案为：+1，-1．
点评：本题考查的是正多边形的性质及勾股定理，根据题意画出图形利用数形结合求解是解答此题的关键．