题目内容
如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形.△OAB的外接圆交y轴的正半轴于点C.(1)点B的坐标是______,点C的坐标是______;
(2)过点C的圆的切线交x轴于点D,则图中阴影部分的面积是______;
(3)若OH⊥AB于点H,点P在线段OH上.点Q在y轴的正半轴上,OQ=PH,PQ与OB交于点M.
①当△OPM为等腰三角形时,求点Q的坐标;
②探究线段OM长度的最大值是多少,直接写出结论.

【答案】分析:(1)由于OA是等边三角形的边,又是圆的弦,过B点作OA的垂线,根据等边三角形的性质,可求B点坐标,连接AC,则∠OCA=∠OBA=60°,解直角△OCA可求OC.
(2)因为∠COA=90°,所以CA为直径,CD为圆的切线,∠OCA=60°,所以∠DCO=30°,解直角△OCD可求OD,取AC的中点(圆心)为O',用阴影部分面积=△OCD面积+△OO'C面积-扇形OO'C面积可求解.
(3)①设点Q的坐标为(0,t),计算OH的长,△OPM为等腰三角形,有三种可能:OP=OM,OM=PM,OP=PM,根据每一种情况下的图形特征,分别求解.
解答: 解:(1)过点B作OA的垂线,垂足为G,
解:(1)过点B作OA的垂线,垂足为G,
∵A(2,0),∴OA=2,OG= OA=1,
OA=1,
设B点坐标为(1,t),则 =2,
=2,
∴t= ,∴B(1,
,∴B(1, )(1分)
)(1分)
连接AC,
则∠OCA=∠OBA=60°,∴ =tan60°,
=tan60°,
OC= =
= =
= ,
,
∴C(0, ).
).
(2)∵∠COA=90°,
∴CA为直径,
又∵CD为圆的切线,∠OCA=60°,
∴∠DCO=30°,
∴OD=tan∠DCO•OC= ×
× =
= ,
,
∵AC是⊙O的直径,BG为△OAB的边OA的中线,
∴O′为△ABC外接圆的圆心,
∵∠OCA=60°,∴∠OCA=30°,∠OO′C=60°,
S阴影=S△OCD+S△OO'C-S扇形OO'C= ×
× ×
× +
+ ×
× ×1-
×1- =
= .
.
(3)①设点Q的坐标为(0,t),
OH=OA×cos60°= ,
,
(I)若OP=OM,∠OPM=∠OMP=75°,
∴∠OQP=45°,
过点P做PE⊥OA,垂足为E,则有:OE= EP,
EP,
即t- (
( -t)=
-t)= (
( t),
t),
解得:t=1,即点Q的坐标为(0,1).
(II)若OM=PM,则∠MOP=∠MPO=30°,
∴PQ∥OA,从而OQ=0.5OP,
即t= (
( -t),
-t),
解得t= 即点的坐标为(0,
即点的坐标为(0, ),
),
(III)若OP=PM,∠POM=∠PMO=∠COB,此时PQ∥OC,不满足题意.
②线段OM的长的最大值为 .
.
点评:本题考查了正三角形与圆,圆的切线性质,等腰三角形条件的探求方法,面积求法及分类讨论的思想,具有较强的综合性.
(2)因为∠COA=90°,所以CA为直径,CD为圆的切线,∠OCA=60°,所以∠DCO=30°,解直角△OCD可求OD,取AC的中点(圆心)为O',用阴影部分面积=△OCD面积+△OO'C面积-扇形OO'C面积可求解.
(3)①设点Q的坐标为(0,t),计算OH的长,△OPM为等腰三角形,有三种可能:OP=OM,OM=PM,OP=PM,根据每一种情况下的图形特征,分别求解.
解答:
 解:(1)过点B作OA的垂线,垂足为G,
解:(1)过点B作OA的垂线,垂足为G,∵A(2,0),∴OA=2,OG=
 OA=1,
OA=1,设B点坐标为(1,t),则
 =2,
=2,∴t=
 ,∴B(1,
,∴B(1, )(1分)
)(1分)连接AC,
则∠OCA=∠OBA=60°,∴
 =tan60°,
=tan60°,OC=
 =
= =
= ,
,∴C(0,
 ).
).(2)∵∠COA=90°,
∴CA为直径,
又∵CD为圆的切线,∠OCA=60°,
∴∠DCO=30°,
∴OD=tan∠DCO•OC=
 ×
× =
= ,
,∵AC是⊙O的直径,BG为△OAB的边OA的中线,
∴O′为△ABC外接圆的圆心,
∵∠OCA=60°,∴∠OCA=30°,∠OO′C=60°,
S阴影=S△OCD+S△OO'C-S扇形OO'C=
 ×
× ×
× +
+ ×
× ×1-
×1- =
= .
.(3)①设点Q的坐标为(0,t),
OH=OA×cos60°=
 ,
,(I)若OP=OM,∠OPM=∠OMP=75°,
∴∠OQP=45°,
过点P做PE⊥OA,垂足为E,则有:OE=
 EP,
EP,即t-
 (
( -t)=
-t)= (
( t),
t),解得:t=1,即点Q的坐标为(0,1).
(II)若OM=PM,则∠MOP=∠MPO=30°,
∴PQ∥OA,从而OQ=0.5OP,
即t=
 (
( -t),
-t),解得t=
 即点的坐标为(0,
即点的坐标为(0, ),
),(III)若OP=PM,∠POM=∠PMO=∠COB,此时PQ∥OC,不满足题意.
②线段OM的长的最大值为
 .
.点评:本题考查了正三角形与圆,圆的切线性质,等腰三角形条件的探求方法,面积求法及分类讨论的思想,具有较强的综合性.

练习册系列答案
相关题目
 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为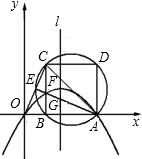 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: