题目内容
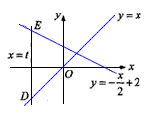
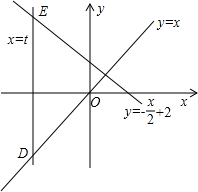 如图,已知平行于y轴的动直线a的解析式为x=t,直线b的解析式为y=x,直线c的解析式为y=-
如图,已知平行于y轴的动直线a的解析式为x=t,直线b的解析式为y=x,直线c的解析式为y=-| 1 | 2 |
分析:由于x=t,分别代入y=x,y=-
x+2,可得E点坐标为(t,-
t+2),D点坐标为(t,t).由于E在D的上方,
故DE=-
t+2-t=-
t+2,且t<
.
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
由于x=t是动直线故应分三种情况讨论:
①t>0时,PE=DE时,PE,DE,PD,分别为斜边的情况;-
t+2=t,求出P点坐标;
②若t<0,PE=DE和PD=DE时;
③若t<0,PE=PD时,即DE为斜边.
| 1 |
| 2 |
| 1 |
| 2 |
故DE=-
| 1 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
由于x=t是动直线故应分三种情况讨论:
①t>0时,PE=DE时,PE,DE,PD,分别为斜边的情况;-
| 3 |
| 2 |
②若t<0,PE=DE和PD=DE时;
③若t<0,PE=PD时,即DE为斜边.
解答: 解:∵当x=t时,y=x=t;当x=t时,y=-
解:∵当x=t时,y=x=t;当x=t时,y=-
x+2
=-
t+2.
∴E点坐标为(t,-
t+2),D点坐标为(t,t).
∵E在D的上方,
∴DE=-
t+2-t
=-
t+2,且t<
.
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
t>0时,PE=DE时,-
t+2=t,
∴t=
,-
t+2=
.∴P点坐标为(0,
).
①若t>0,PD=DE时,-
t+2=t,
∴t=
.∴P点坐标为(0,
).
②若t>0,PE=PD时,即DE为斜边,∴-
t+2=2t
∴t=
,DE的中点坐标为(t,
t+1),∴P点坐标为(0,
).
若t<0,PE=DE和PD=DE时,由已知得DE=-t,-
t+2=-t,t=4>0
(不符合题意,舍去),
此时直线x=t不存在.
③若t<0,PE=PD时,即DE为斜边,由已知得DE=-2t,-
t+2=-2t,
∴t=-4,
t+1=0,∴P点坐标为(0,0)
综上所述:当t=
时,△PDE为等腰直角三角形,此时P点坐标为或(0,
);
当t=
时,△PDE为等腰直角三角形,此时P点坐标为(0,
);
当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
 解:∵当x=t时,y=x=t;当x=t时,y=-
解:∵当x=t时,y=x=t;当x=t时,y=-| 1 |
| 2 |
=-
| 1 |
| 2 |
∴E点坐标为(t,-
| 1 |
| 2 |
∵E在D的上方,
∴DE=-
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 4 |
| 3 |
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
t>0时,PE=DE时,-
| 3 |
| 2 |
∴t=
| 4 |
| 5 |
| 1 |
| 2 |
| 8 |
| 5 |
| 8 |
| 5 |
①若t>0,PD=DE时,-
| 3 |
| 2 |
∴t=
| 4 |
| 5 |
| 4 |
| 5 |
②若t>0,PE=PD时,即DE为斜边,∴-
| 3 |
| 2 |
∴t=
| 4 |
| 7 |
| 1 |
| 4 |
| 8 |
| 7 |
若t<0,PE=DE和PD=DE时,由已知得DE=-t,-
| 3 |
| 2 |
(不符合题意,舍去),
此时直线x=t不存在.
③若t<0,PE=PD时,即DE为斜边,由已知得DE=-2t,-
| 3 |
| 2 |
∴t=-4,
| 1 |
| 4 |
综上所述:当t=
| 4 |
| 5 |
| 4 |
| 5 |
当t=
| 4 |
| 7 |
| 8 |
| 7 |
当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
点评:本题把动直线与等腰直角三角形的性质结合起来,解答此类问题时要注意分类讨论,不要漏解.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,已知平行于y轴的动直线a的解析式为x=t,直线b的解析式为y=x,直线c的解析式为y=-
如图,已知平行于y轴的动直线a的解析式为x=t,直线b的解析式为y=x,直线c的解析式为y=- x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.
x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________. x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是 .
x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是 .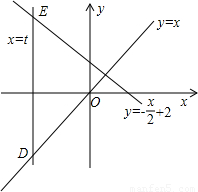
 x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是 .
x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是 .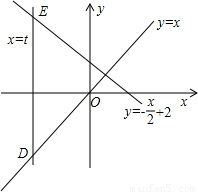
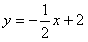 且动直线分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足
且动直线分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足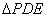 是等腰直角三角形,则点P的坐标是( )
是等腰直角三角形,则点P的坐标是( )