题目内容
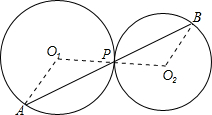
如图，在⊙O的内接△ABC中，AB=AC，D是⊙O上一点，AD的延长线交BC的延长线于点P．
（1）求证：AB2=AD•AP；
（2）若⊙O的直径为25，AB=20，AD=15，求PC和DC的长．
（1）求证：AB2=AD•AP；
（2）若⊙O的直径为25，AB=20，AD=15，求PC和DC的长．
（1）证明：∵∠ADC+∠B=180°，∠B=∠ACB
∴∠ACP+∠ACB=∠ACP+∠B=180°
∴∠ADC=∠ACP
∴△ADC∽△ACP
∴
=
，即
=
所以AB2=AD•AP；
（2）过点A作直径AE交BC于点F．
∵△ABC是等腰三角形，
∴AE垂直平分BC
设AF=a，则EF=25-a，BF=
由BF2=AF•EF，得400-a2=a（25-a）
所以AF=a=16，BF=FC=12．
方法1：
由（1）AB2=AD•AP得：AP=
=
=
在Rt△AFP中，PF=
=
=
∴PC=PF-FC=
-12=
又由△PCD∽△PAB得：
=
∴DC=
=
=7；
方法2：（前面部分给分相同）连接BE、EC、BD．
∵AE是直径，
∴∠ABE=90°，且BE=
=15
∴EC=BE=15，又已知AD=15，∴AD=EC
∴DC∥AE，即DC⊥BC，则BD是直径
∴DC=
=
=7
在Rt△PCD中，PD=PA-AD=
-15=
∴PC=
=
．
∴∠ACP+∠ACB=∠ACP+∠B=180°
∴∠ADC=∠ACP
∴△ADC∽△ACP
∴
| AD |
| AC |
| AC |
| AP |
| AD |
| AB |
| AB |
| AP |
所以AB2=AD•AP；
（2）过点A作直径AE交BC于点F．
∵△ABC是等腰三角形，
∴AE垂直平分BC
设AF=a，则EF=25-a，BF=
| 400-a2 |
由BF2=AF•EF，得400-a2=a（25-a）
所以AF=a=16，BF=FC=12．
方法1：
由（1）AB2=AD•AP得：AP=
| AB2 |
| AD |
| 400 |
| 15 |
| 80 |
| 3 |
在Rt△AFP中，PF=
| AP2-AF2 |
(
|
| 64 |
| 3 |
∴PC=PF-FC=
| 64 |
| 3 |
| 28 |
| 3 |
又由△PCD∽△PAB得：
| DC |
| AB |
| PC |
| PA |
∴DC=
| PC•AB |
| PA |
| 28×20 |
| 80 |
方法2：（前面部分给分相同）连接BE、EC、BD．
∵AE是直径，
∴∠ABE=90°，且BE=
| 252-202 |
∴EC=BE=15，又已知AD=15，∴AD=EC
∴DC∥AE，即DC⊥BC，则BD是直径
∴DC=
| BD2-BC2 |
| 252-242 |
在Rt△PCD中，PD=PA-AD=
| 80 |
| 3 |
| 35 |
| 3 |
∴PC=
(
|
| 28 |
| 3 |
练习册系列答案
相关题目
半圆，EF是这两个半圆的外公切线，E、F为切点．
