题目内容
抛物线y=x2-4x-5与x轴的正半轴的交点坐标为________，与y轴的交点坐标为________．
（5，0） （0，-5）
分析：令y=0，可求抛物线与x轴的交点坐标；令x=0，可求抛物线与y轴的交点坐标．
解答：当x=0时，y=-5，即与y轴的交点坐标是（0，-5）；
当y=0时，x=5或-1，所以与x轴正半轴的交点坐标是（5，0）．
点评：主要考查了二次函数图象与（x轴）y轴的交点坐标特点．
分析：令y=0，可求抛物线与x轴的交点坐标；令x=0，可求抛物线与y轴的交点坐标．
解答：当x=0时，y=-5，即与y轴的交点坐标是（0，-5）；
当y=0时，x=5或-1，所以与x轴正半轴的交点坐标是（5，0）．
点评：主要考查了二次函数图象与（x轴）y轴的交点坐标特点．
练习册系列答案
相关题目
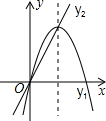如图，抛物线y1=-x2+4x和直线y2=2x．当y1＞y2时，x的取值范围是（ ）| A、0＜x＜2 | B、x＜0或x＞2 | C、x＜0或x＞4 | D、0＜x＜4 |