��Ŀ����
����Ŀ���Ķ�������ϣ�
��ͼ![]() ����
����![]() ��ֱ��
��ֱ��![]() ƽ���ƶ��߶�
ƽ���ƶ��߶�![]() �ij��ȣ����Ա䵽
�ij��ȣ����Ա䵽![]() ��λ�ã�
��λ�ã�
��ͼ![]() ����
����![]() Ϊ�ᣬ��
Ϊ�ᣬ��![]() ����
����![]() �����Ա䵽
�����Ա䵽![]() ��λ�ã�
��λ�ã�
��ͼ![]() ���Ե�
���Ե�![]() Ϊ���ģ���
Ϊ���ģ���![]() ��ת
��ת![]() �����Ա䵽
�����Ա䵽![]() ��λ�ã�
��λ�ã�
������������һ��������������һ�������ΰ�ƽ���ƶ������ۡ���ת�ȷ�����ɵģ�����ֻ�ı�λ�ã����ı���״��С��ͼ�α任�����������ε�ȫ�ȱ任��
�ش��������⣺
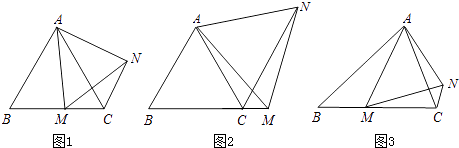
����ͼ![]() �У�����ͨ��ƽ���ƶ������ۡ���ת�е���һ�ַ��������仯��ʹ
�У�����ͨ��ƽ���ƶ������ۡ���ת�е���һ�ַ��������仯��ʹ![]() �䵽
�䵽![]() ��λ�ã�
��λ�ã�
��ָͼ���߶�![]() ��
��![]() ֮��Ĺ�ϵ��Ϊʲô��
֮��Ĺ�ϵ��Ϊʲô��

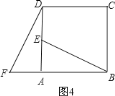
���𰸡�����ͼ![]() �п���ͨ����ת
�п���ͨ����ת![]() ʹ
ʹ![]() �䵽
�䵽![]() ��λ������֤��������.
��λ������֤��������.
��������
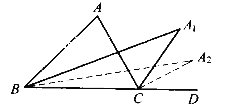
��AB��AD�Ƕ�Ӧ�߶Σ���ôӦ�Ƶ�A��ʱ����ת90��õ���
�ڹ�ϵӦ����λ�ù�ϵ��������ϵ����תǰ�����������ȫ�ȵģ���BE=DF���ӳ�BE��DF�ڵ�G�����ö�Ӧ����ȣ��ɵõ���ֱ��
����ͼ![]() �п���ͨ����ת
�п���ͨ����ת![]() ʹ
ʹ![]() �䵽
�䵽![]() ��λ�ã�
��λ�ã�
����ȫ�ȱ任�Ķ����֪��ͨ����ת![]() ��
��![]() �䵽
�䵽![]() ��λ�ã�ֻ�ı�λ�ã����ı���״��С��
��λ�ã�ֻ�ı�λ�ã����ı���״��С��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��

��ϰ��ϵ�д�
 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
�����Ŀ