题目内容
四边形ABCD中,AD∥BC,∠ABC=80°,AD=AB= BC,CH⊥AB于H.连接DH,则∠CHD的度数为
BC,CH⊥AB于H.连接DH,则∠CHD的度数为
- A.30°
- B.35°
- C.40°
- D.45°
C
分析:首先作出图形,过点D作DE平行于AB交BC于点E,连接DH,根据四边形ABCD中,AD∥BC,AD=AB,证明四边形ABED是菱形,即可得到DE=EC,再根据题干条件得到∠EDC=∠ECD,最后根据AD=AB= BC,可得点E是BC的中点,得到DE平分CH,又∵DE平行于AB,所以DE垂直于CH,也就是DE垂直平分CH,于是得到∠CHD=∠DCH=40°.
BC,可得点E是BC的中点,得到DE平分CH,又∵DE平行于AB,所以DE垂直于CH,也就是DE垂直平分CH,于是得到∠CHD=∠DCH=40°.
解答: 解:作出图形,过点D作DE平行于AB交BC于点E,
解:作出图形,过点D作DE平行于AB交BC于点E,
∵四边形ABCD中,AD∥BC,AD=AB,
∴四边形ABED是菱形,
∴DE=EC,
∵∠ABC=80°,
∴∠DEC=80°,
∴∠EDC=∠ECD= =50°,
=50°,
∵CH⊥AB于H,
∴∠BCH=10°,从而得到∠DCH=40°,
根据AD=AB= BC,可得点E是BC的中点,
BC,可得点E是BC的中点,
∴DE平分CH,
又∵DE平行于AB,
所以DE垂直于CH,也就是DE垂直平分CH,
∴∠CHD=∠DCH=40°.
故选C.
点评:本题主要考查平行四边形和等腰三角形的判定与性质和直角三角形斜边中线的知识点,解答本题的关键是求出DE=CE,此题难度一般.
分析:首先作出图形,过点D作DE平行于AB交BC于点E,连接DH,根据四边形ABCD中,AD∥BC,AD=AB,证明四边形ABED是菱形,即可得到DE=EC,再根据题干条件得到∠EDC=∠ECD,最后根据AD=AB=
 BC,可得点E是BC的中点,得到DE平分CH,又∵DE平行于AB,所以DE垂直于CH,也就是DE垂直平分CH,于是得到∠CHD=∠DCH=40°.
BC,可得点E是BC的中点,得到DE平分CH,又∵DE平行于AB,所以DE垂直于CH,也就是DE垂直平分CH,于是得到∠CHD=∠DCH=40°.解答:
 解:作出图形,过点D作DE平行于AB交BC于点E,
解:作出图形,过点D作DE平行于AB交BC于点E,∵四边形ABCD中,AD∥BC,AD=AB,
∴四边形ABED是菱形,
∴DE=EC,
∵∠ABC=80°,
∴∠DEC=80°,
∴∠EDC=∠ECD=
 =50°,
=50°,∵CH⊥AB于H,
∴∠BCH=10°,从而得到∠DCH=40°,
根据AD=AB=
 BC,可得点E是BC的中点,
BC,可得点E是BC的中点,∴DE平分CH,
又∵DE平行于AB,
所以DE垂直于CH,也就是DE垂直平分CH,
∴∠CHD=∠DCH=40°.
故选C.
点评:本题主要考查平行四边形和等腰三角形的判定与性质和直角三角形斜边中线的知识点,解答本题的关键是求出DE=CE,此题难度一般.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.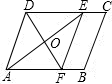 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.