题目内容
【题目】若关于![]() 的二次函数
的二次函数![]() (
(![]() 为常数)与
为常数)与![]() 轴交于两个不同的点
轴交于两个不同的点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其图象的顶点为点
,其图象的顶点为点![]() 是坐标原点.
是坐标原点.
(1)若![]() 、
、![]() 、
、![]() ,求此二次函数的解析式并写出二次函数的对称轴;
,求此二次函数的解析式并写出二次函数的对称轴;
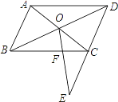
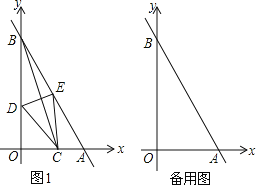
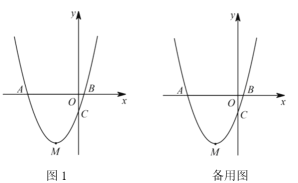
(2)如图1,若![]() ,
,![]() ,
,![]() 为直角三角形,
为直角三角形,![]() 是以
是以![]() 的等边三角形,试确定
的等边三角形,试确定![]() 的值;
的值;
(3)设![]() 为正整数,且
为正整数,且![]() ,
,![]() ,
,![]() 为任意常数,令
为任意常数,令![]() ,
,![]() ,如果对于一切实数
,如果对于一切实数![]() ,
,![]() 始终成立,求
始终成立,求![]() 的值.
的值.
【答案】(1)![]() ,对称轴
,对称轴![]() ;(2)
;(2)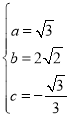 ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)函数的表达式为:y=a(x+2)(x-4)=a(x2-2x-8),即可求解;
(2)设![]() ,
,![]() ,
,![]() ,由
,由![]() ,得到
,得到![]() ,结合一元二次方程根与系数的关系,得到
,结合一元二次方程根与系数的关系,得到![]() ;由
;由![]() 为边长2的等边三角形,则
为边长2的等边三角形,则![]() ,得到
,得到![]() ;由
;由![]() ,得到
,得到![]() ,联立方程组,即可求出a、b、c的值.
,联立方程组,即可求出a、b、c的值.
(3)先表示出解析式,求出点A、B的横坐标,得到AB=x2-x1=|mt+3|≥|2t+n|,对于一切实数t,上式都成立,则必然存在|mt+3|=|2t+n|,结合一元二次方程根的判别式即可求解.
解:(1)设函数的表达式为:y=a(x+2)(x-4)=a(x2-2x-8),
把点C代入,则-8a=3,
解得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴对称轴![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,
,
∵![]() 为直角三角形,且
为直角三角形,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,
,![]() ,
,
则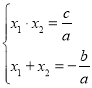 ,
,
∴![]() ,
,
∴![]() ①;
①;
又∵![]() 为边长2的等边三角形,
为边长2的等边三角形,
∴抛物线顶点坐标中纵坐标为![]() ,且
,且![]() .
.
∴![]() ,
,
∴![]() ②;
②;
又∵![]()
∴![]() ③
③
由①②③得: ,
,
解得: ;
;
(3)根据题意,解析式:![]() .
.
令![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴AB=![]() ;
;
∴![]() (两边平方),
(两边平方),
∴![]() ,
,
∴![]() ,
,
∴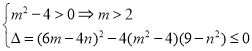 恒成立.
恒成立.
∴![]() ,
,
∴![]() 且
且![]() 为正整数
为正整数
∴![]() 或
或![]() .
.

练习册系列答案
相关题目