题目内容
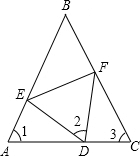 如图,点D、F、E分别在△ABC的三边上,∠1=∠2=∠3,DE=DF,请你说明△ADE≌△CFD的理由.
如图,点D、F、E分别在△ABC的三边上,∠1=∠2=∠3,DE=DF,请你说明△ADE≌△CFD的理由.
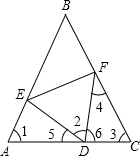 解:∵∠4+∠6=180°-∠3,∠5+∠6=180°-∠2,∠3=∠2,
解:∵∠4+∠6=180°-∠3,∠5+∠6=180°-∠2,∠3=∠2,∴∠4+∠6=∠5+∠6,
∴∠4=∠5,
∵在△ADE和△CFD中,
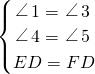 ,
,∴△ADE≌△CFD(AAS).
分析:首先根据三角形内角和公式可得∠4+∠6=180°-∠3,再根据平角定义可得∠5+∠6=180°-∠2,再由∠3=∠2,可得∠4=∠5,然后加上条件∠1=∠3,DE=DF可利用AAS证明△ADE≌△CFD.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
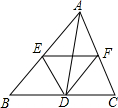 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )