题目内容
【题目】如图,△ABC的面积为18,BD=2DC,AE=EC,那么阴影部分的面积是_______.

【答案】![]()
【解析】分析:作DG∥AC,交BE于点G,设阴影部分的面积a,由相似三角形的面积比等于对应边长比的平方得出△BGD的面积,△GDF的面积,再利用△BGD的面积+△GDF的面积+阴影部分的面积a=9,列出方程求解即可得出答案.
本题解析: 如图:
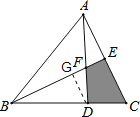
作DG∥AC,交BE于点G,设阴影部分的面积a,
∵DG∥AC,BD=2DC,
∴GD=![]() EC,BD=
EC,BD=![]() BC,
BC,
∴△BGD的面积=![]() △BCE的面积,
△BCE的面积,
∵△ABC的面积为18,AE=EC,
∴△BCE的面积=![]() △ABC的面积=9,
△ABC的面积=9,
∴△BGD的面积=![]() △BCE的面积=4,
△BCE的面积=4,
又∵△GDF∽△EAF,且![]() =
=![]() ,
,
∴△GDF的面积=![]() △EAF的面积,
△EAF的面积,
∵BD=2DC,
∴△ADC的面积=18×![]() =6,
=6,
∴△EAF的面积=6a,
∴△GDF的面积=![]() △EAF的面积=
△EAF的面积=![]() (6a),
(6a),
∴△BGD的面积+△GDF的面积+阴影部分的面积a=9,
∴4+![]() (6a)+a=9,解得a=
(6a)+a=9,解得a=![]() .
.
故答案为: ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
