Question

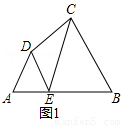
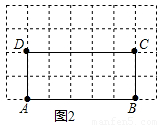
阅读理解：如图1，在直角梯形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，易证△ABP∽△PCD，从而得到BP•PC=AB•CD，解答下列问题．
（1）模型探究：如图2，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，结论BP•PC=AB•CD仍成立吗？试说明理由；
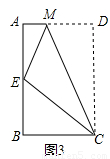
（2）拓展应用：如图3，M为AB的中点，AE与BD交于点C，∠DME=∠A=∠B=45°且DM交AC于F，ME交BC于G．AB=，AF=3，求FG的长．

Answer 1

【答案】分析：（1）通过相似三角形△ABP∽△PCD的对应边成比例来证得BP•PC=AB•CD；
（2）利用相似三角形△AMF∽△BGM的对应角相等、三角形内角和定理证得AC⊥BC且AC=BC；然后在直角△ABC中由勾股定理求得AC=BC=4；最后利用相似三角形△AMF∽△BGM的对应边成比例以及在直角△FCG中利用勾股定理来求FG的长度．
解答：解：（1）∵∠APC=∠APD+∠CPD，∠APC=∠BAP+∠B（三角形外角定理），∠B=∠APD（已知），
∴∠BAP=∠CPD，
又∵∠B=∠C，
∴△ABP∽△PCD
∴=，
∴BP•PC=AB•CD；

（2）∵∠AFM=∠DME+∠E（三角形外角定理），∠DME=∠A（已知），
∴∠AFM=∠A+∠E（等量代换），
又∠BMG=∠A+∠E（三角形外角定理），
∴∠AFM=∠BMG．
∵∠A=∠B，
∴△AMF∽△BGM．
当∠A=∠B=45°时，∠ACB=180°-∠A-∠B=90°，即AC⊥BC且AC=BC．
∵M为AB的中点，∴AM=BM=，AC=BC=4．
又∵△AMF∽△BGM，
∴，
∴BG===，
又∵，CF=4-3=1，
∴．
点评：本题考查了相似综合题．此题综合运用了相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角定理．