题目内容
1. 如图,在四边形ABCD中,∠A=∠C=90゜.若BE、DF分别平分∠ABC、∠ADC的外角,问BE与DF的位置关系,并证明.
如图,在四边形ABCD中,∠A=∠C=90゜.若BE、DF分别平分∠ABC、∠ADC的外角,问BE与DF的位置关系,并证明.
分析 连接BD,根据四边形内角和为360°可得∠NDC+∠MBC=180゜,则可得∠FDC+∠CBE=90゜,继而可证得∠FDC+∠CDB+∠CBD+∠EBC=180゜,则可得DE∥BF.
解答  解:DE∥BF,
解:DE∥BF,
理由:连接BD,
∵∠A=∠C=90゜,
∴∠ABC+∠ADC=180°,
∴∠NDC+∠MBC=180゜,
∵BE、DF分别平分∠ABC、∠ADC的外角,
∴∠FDC+∠CBE=90゜,
∴∠FDC+∠CDB+∠CBD+∠EBC=180゜,
∴DE∥BF.
点评 此题主要考查了平行线的判定,关键是掌握同旁内角互补,两直线平行.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
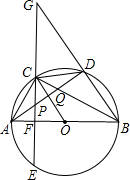 已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q.则下列说法中正确的个数为( )
已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q.则下列说法中正确的个数为( )


