题目内容
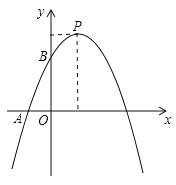
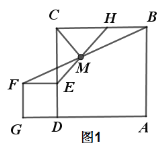
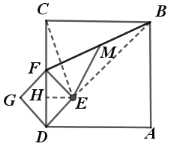
【题目】如图1,点E是正方形ABCD边CD上任意点,以DE为边作正方形DEFG,连接BF.点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系:__________;
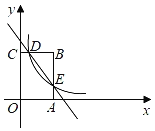
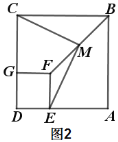
(2)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图2所示,其他条件不变,(1)中的结论是否成立,请说明理由.
(3)若DG=![]() ,AB=4.
,AB=4.
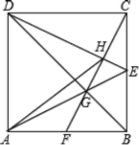
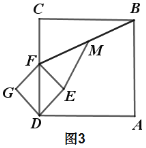
①把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,连接EM,如图3所示,其他条件不变,计算EM的长度;
②若把图1中的正方形DEFG绕点D顺时针旋转一周,请直接写出EM的最大值.
【答案】(1)![]() .(2)成立,具体利用见解析;(3)①
.(2)成立,具体利用见解析;(3)①![]() ;②
;②![]() .
.
【解析】
(1)证明![]() ,得到HM=EM,根据等腰之间三角形的性质即可得到;
,得到HM=EM,根据等腰之间三角形的性质即可得到;
(2)连接DF,MG,作![]() 于N,可证得
于N,可证得![]() ,得到ME=MG,
,得到ME=MG,![]() ,再由M为BF的中点,
,再由M为BF的中点,![]() ,得到GN=NC,进一步可得到,又
,得到GN=NC,进一步可得到,又![]() ,
,![]() ,再由角度的关系可得到
,再由角度的关系可得到![]() ,即可得到结论.
,即可得到结论.
(3)①连接BE,CE,过点E作![]() 于点H,根据正方形的性质可推出
于点H,根据正方形的性质可推出![]() ,
,![]() ,证明
,证明![]() ,进一步可得到△CME是等腰直角三角形,根据之间三角形的性质求解即可.
,进一步可得到△CME是等腰直角三角形,根据之间三角形的性质求解即可.
②由条件可证的△CME为等腰直角三角形,当CE最大时,EM最大,当点E旋转至D点下方时,且C,D,E共线时CE最大,此时CE=![]() ,再根据勾股定理即可求解.
,再根据勾股定理即可求解.
(1)结论:![]() .
.
理由:如图1中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在△FME和△BMH中,
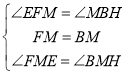 ,
,
∴![]() ,
,
∴HM=EM,EF=BH.
∵CD=BC,
∴CE=CH,
又∵![]() ,HM=EM,
,HM=EM,
∴![]() .
.
(2)![]() .
.
理由:如图,连接DF,MG,作![]() 于N,
于N,
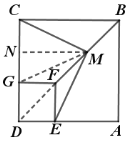
在△EDM和△GDM中,
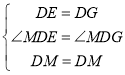 ,
,
∴![]() ,
,
∴ME=MG,![]() ,
,
∵M为BF的中点,![]() ,
,
∴GN=NC,
又![]() ,
,
∴MC=ME,
∴MC=MG,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴(1)中结论成立.
(3)①解:如图,连接BE,CE,过点E作![]() 于点H,
于点H,
∵四边形ABCD和四边形EDGH是正方形,
∴![]() ,
,![]() ,
,
∴点B、E、D在同一条直线上,
∵![]() ,
,![]() ,M为BF的中点,
,M为BF的中点,
∴![]() ,
,![]() ,
,
∴CM=ME,
又∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△CME是等腰直角三角形,![]() ,
,
在Rt△CME中,![]() ,
,![]() ,
,
∴EH=DH=1,
∴CH=4-1=3,
在Rt△CHE中,![]() ,
,
∴![]() .
.
②由上问可知![]() 一直成立,
一直成立,
∴△CME为等腰直角三角形,
∴当CE最大时,EM最大,
当点E旋转至D点下方时,且C,D,E共线时CE最大,
此时CE=![]() .
.
设CM=EM=x,
则![]() ,
,
解得![]() ,
,
∴EM的最大值为![]() .
.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
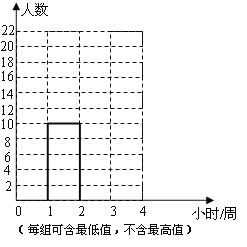
(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?