题目内容
已知a、b、c是Rt△ABC三边的长,a<b<c,(1)求证:关于x的方程a(1-x2)-2
| 2 |
(2)若c=3a,x1,x2是这个方程的两根,求x12+x22的值.
分析:(1)要证明方程有两个不相等的实数根,即证明△>0即可,(2)根据方程的两个实数根为x1和x2,写出两根之和和两根之积,即可求出x12+x22的值.
解答:解:(1)把方程a(1-x2)-2
bx+c(1+x2)=0化成一般形式为(c-a)x2-2
bx+a+c=0,
故方程根的判别式△=8b2-4a2+4c2,
∵a、b、c是Rt△ABC三边的长,
∵a<b<c,
∴△=8b2-4a2+4c2>0,
∴方程a(1-x2)-2
bx+c(1+x2)=0有两个不相等的实数根;
(2)∵x1+x2=
,x1•x2=
,
∵c=3a,
∴x1+x2=
,x1•x2=2,
∴x12+x22=
-4.
| 2 |
| 2 |
故方程根的判别式△=8b2-4a2+4c2,
∵a、b、c是Rt△ABC三边的长,
∵a<b<c,
∴△=8b2-4a2+4c2>0,
∴方程a(1-x2)-2
| 2 |
(2)∵x1+x2=
2
| ||
| c-a |
| a+c |
| c-a |
∵c=3a,
∴x1+x2=
| ||
| a |
∴x12+x22=
| 2b2 |
| a2 |
点评:本题主要考查了一元二次方程根与系数的关系和根的判别式的知识点,熟练掌握若x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q,方程总有两个实数根,则一元二次方程根的判别式△>0恒成立.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
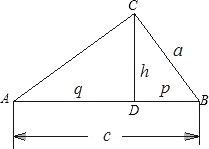 已知:如图,CD是Rt△ABC的斜边AB上的高,且BC=a,AB=c,CD=h,AD=q,DB=p.求证:h2=p•q,a2=p•c.
已知:如图,CD是Rt△ABC的斜边AB上的高,且BC=a,AB=c,CD=h,AD=q,DB=p.求证:h2=p•q,a2=p•c. 已知:如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.求证:CE2=ED•EP.
已知:如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.求证:CE2=ED•EP. 已知:如图,AD是Rt△ABC的角平分线,AD的垂直平分线EF交CB的延长线于点F,求证:FD2=FB•FC.
已知:如图,AD是Rt△ABC的角平分线,AD的垂直平分线EF交CB的延长线于点F,求证:FD2=FB•FC. 已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,AD∥BC.
已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,AD∥BC.