题目内容
 (1)计算:
(1)计算: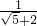 +(-3)0
+(-3)0
(2)如图所示,△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,若AC= .求线段AD的长.
.求线段AD的长.
解:(1)原式=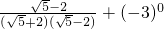
=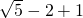
= -1.
-1.
(2)∵△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD是△ABC的角平分线,
∴∠CAD=30°.
∴在Rt△ADC中,
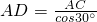
= ×
×
=2.
分析:(1)根据分母有理化和零指数幂进行计算;
(2)先求∠BAC=60°,再由AD是△ABC的角平分线,求得∠CAD=30°,利用三角函数求AD的长.
点评:本题考查了分母有理化和零指数幂的计算以及解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
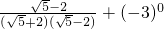
=
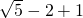
=
 -1.
-1. (2)∵△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD是△ABC的角平分线,
∴∠CAD=30°.
∴在Rt△ADC中,
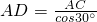
=
 ×
×
=2.
分析:(1)根据分母有理化和零指数幂进行计算;
(2)先求∠BAC=60°,再由AD是△ABC的角平分线,求得∠CAD=30°,利用三角函数求AD的长.
点评:本题考查了分母有理化和零指数幂的计算以及解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.

练习册系列答案
相关题目
