题目内容
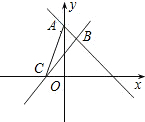 如图,直线y=-
如图,直线y=-| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
分析:根据题意分别求出A,B,C,D的坐标,再用S△ACD-S△BCD即可求出△ABC的面积.
解答: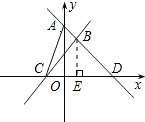 解:因为直线y=-
解:因为直线y=-
x+4中,b=4,故A点坐标为(0,4);
令-
x+4=0,则x=3,故D点坐标为(3,0).
令
x+
=0,则,x=-1,故C点坐标为(-1,0),
因为B点为直线y=-
x+4直线y=
x+
的交点,
故可列出方程组
,解得
,故B点坐标为(
,2),
故S△ABC=S△ACD-S△BCD=
CD•AO-
CD•BE=
×4×4-
×4×2=4.
 解:因为直线y=-
解:因为直线y=-| 4 |
| 3 |
令-
| 4 |
| 3 |
令
| 4 |
| 5 |
| 4 |
| 5 |
因为B点为直线y=-
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
故可列出方程组
|
|
| 3 |
| 2 |
故S△ABC=S△ACD-S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 12、如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2=
12、如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2=
 20、如图,直线AB∥CD,EF⊥AB,垂足为O,FG与CD相交于H,若∠1=43°,则∠2=
20、如图,直线AB∥CD,EF⊥AB,垂足为O,FG与CD相交于H,若∠1=43°,则∠2=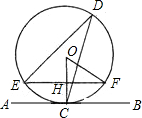 如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连接DE、DC、OF.
如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连接DE、DC、OF.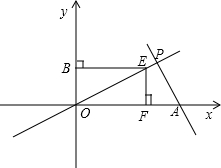 已知如图,直线y=-
已知如图,直线y=-