题目内容
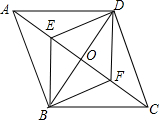 如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )
如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )| A、5个 | B、4个 | C、3个 | D、2个 |
分析:①正确,根据三角形的面积公式可得到结论.
②根据已知条件利用菱形的判定定理可证得其正确.
③正确,根据菱形的面积等于对角线乘积的一半即可求得.
④不正确,根据已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确,由已知可证得△DEO≌△DFO,从而可推出结论正确.
②根据已知条件利用菱形的判定定理可证得其正确.
③正确,根据菱形的面积等于对角线乘积的一半即可求得.
④不正确,根据已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确,由已知可证得△DEO≌△DFO,从而可推出结论正确.
解答:解:①正确
∵E、F分别是OA、OC的中点.
∴AE=OE.
∵S△ADE=
×AE×OD=
×OE×OD=S△EOD
∴S△ADE=S△EOD.
②正确
∵四边形ABCD是菱形,E,F分别是OA,OC的中点.
∴EF⊥OD,OE=OF.
∵OD=OD.
∴DE=DF.
同理:BE=BF
∴四边形BFDE是菱形.
③正确
∵菱形ABCD的面积=
AC×BD.
∵E、F分别是OA、OC的中点.
∴EF=
AC.
∴菱形ABCD的面积=EF×BD.
④不正确
由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确
∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.
∴△DEF是轴对称图形.
∴正确的结论有四个,分别是①②③⑤,故选B.
∵E、F分别是OA、OC的中点.
∴AE=OE.
∵S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADE=S△EOD.
②正确
∵四边形ABCD是菱形,E,F分别是OA,OC的中点.
∴EF⊥OD,OE=OF.
∵OD=OD.
∴DE=DF.
同理:BE=BF
∴四边形BFDE是菱形.
③正确
∵菱形ABCD的面积=
| 1 |
| 2 |
∵E、F分别是OA、OC的中点.
∴EF=
| 1 |
| 2 |
∴菱形ABCD的面积=EF×BD.
④不正确
由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确
∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.
∴△DEF是轴对称图形.
∴正确的结论有四个,分别是①②③⑤,故选B.
点评:此题主要考查学生对菱形的性质等知识的理解及运用能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ( )
( ) 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
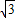 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.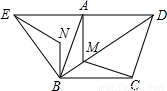
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.