题目内容
在Rt△ABC中，已知∠C=90°，sinA=
，求cosA、tanA以及∠B的三个三角函数值．
解：
∵sinA==
，
∴设BC=3k，AB=5k，由勾股定理得：AC=4k，
则cosA=
=
=
，
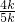tanA=
=
=
，
sinB==，
cosB==，tanB=
=
．
分析：根据已知角A的正弦设设BC=3k，得出AB=5k，由勾股定理求出AC=4k，根据锐角三角函数的定义求出即可．
点评：本题考查了锐角三角函数的定义的应用，注意：在Rt△ACB中，∠C=90°，则sinA=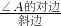
，cosA=
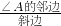，tanA=
．
∵sinA=
=，∴设BC=3k，AB=5k，由勾股定理得：AC=4k，
则cosA=
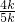==，tanA=
==，sinB=
=，cosB=
=，tanB==．分析：根据已知角A的正弦设设BC=3k，得出AB=5k，由勾股定理求出AC=4k，根据锐角三角函数的定义求出即可．
点评：本题考查了锐角三角函数的定义的应用，注意：在Rt△ACB中，∠C=90°，则sinA=
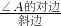，cosA=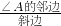，tanA=． 
练习册系列答案
天天练口算系列答案
相关题目
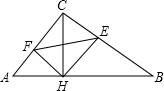如图，在Rt△ABC中，已知∠ACB=90°，且CH⊥AB，HE⊥BC，HF⊥AC．
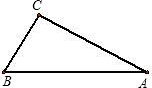如图，在Rt△ABC中，已知∠BCA=90°，∠BAC=30°，AB=6cm．把△ABC以点B为中心逆时针旋转，使点C旋转到AB边的延长线上得到Rt△A1BC1．在Rt△ABC中，已知∠C=90°，∠A=30°，BD是∠B的平分线，AC=18，则BD的值为（ ）
A、3
| ||
| B、9 | ||
| C、12 | ||
| D、6 |
如图，在Rt△ABC中，已知∠ABC=90°，BC=6，以AB为直径作⊙O，连接OC，过点C作⊙O的切线CD，D为切点，若sin∠OCD=
如图，在Rt△ABC中，已知tanB=2，则sinA的值是（ ）