Question

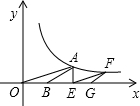如图，钝角等腰三角形AOB，EFG的顶点O，B，E在x轴上，A，F在函数y=

4 3

x

(x＞0)图象上，且AE垂直x轴于点E，∠ABO=∠FGE=120°，则F点的坐标为（　　）

• A、(

  5 +1

  2

  ，

  5 -1

  2

  )
• B、(

  15

  +

  3

  ，

  5

  -1)
• C、(

  3+ 15

  2

  ，

  5 + 3

  2

  )
• D、(

  5 -1

  2

  ，

  3

  2

  )

Answer 1

分析：此题可先由△OAE及A点在函数图象上求得A点坐标，再设出F点坐标，由两钝角等腰三角形相似求得F点坐标．

解答：解：作FD垂直于x轴于D．
由于钝角等腰三角形AOB，则OB=BA，AE垂直x轴于点E，∠ABO=∠FGE=120°，
则A（2

3

，2）．
由于两钝角等腰三角形相似，设ED=

3

x，FD=x，
则F（2

3

+

3

x，x），则代入函数y=

4 3

x

(x＞0)得：
x（2

3

+

3

x）=4

3

，解得：x=

5

-1．
则2

3

+

3

x=

15

+

3

，F(

15

+

3

，

5

-1)．
故选B．

点评：本题考查了钝角三角形的性质与反比例函数性质的综合应用，体现了数学上数形结合的思想．