题目内容
已知:在直角坐标系中,直线 y=2x+2与x轴交于点A,与y轴交于点B。
(1)画出这个函数的图象,并直接写出两点A,B的坐标;
(2)若点C是第二象限内的点,且到x轴的距离为1,到y轴的距离为 ,请判断点C是否在这条直线上?(写出判断过程)
,请判断点C是否在这条直线上?(写出判断过程)
(3)在第(2)题中,作CD ⊥ x轴于D,那么在x轴上是否存在一点P,使△CDP≌△AOB?若存在,请求出点P的坐标;若不存在,请说明理由。
(1)画出这个函数的图象,并直接写出两点A,B的坐标;
(2)若点C是第二象限内的点,且到x轴的距离为1,到y轴的距离为
 ,请判断点C是否在这条直线上?(写出判断过程)
,请判断点C是否在这条直线上?(写出判断过程)(3)在第(2)题中,作CD ⊥ x轴于D,那么在x轴上是否存在一点P,使△CDP≌△AOB?若存在,请求出点P的坐标;若不存在,请说明理由。

(1)如图

(2)可设C点坐标为(m, n) ∵C到轴的距离为1,到轴的距离为 ∴|m| =  , |n| = 1
, |n| = 1
∴ m = ± ,n = ± 1
,n = ± 1
∵ 点是第二象限内的点 ∴C点坐标为(- , 1)
, 1)
点当x = - 时, y = -
时, y = - ×2 = 1 ∴点C在直线
×2 = 1 ∴点C在直线 上
上
(3)存在, ∵ |CD| =1,|OA| = 1,
∴ |CD| = |OA|
又∵点P在x轴上
∴∠CDP = 90°= ∠AOB 若 |DP| = |OB| = 2 时,可用SAS证明△CDP≌△AOB,
∴当P点坐标为(- +2,0)或(-
+2,0)或(- -2,0)时, 即P点坐标为(
-2,0)时, 即P点坐标为( ,0)或(-
,0)或(- ,0)时,
,0)时,
△CDP≌△AOB

练习册系列答案
相关题目
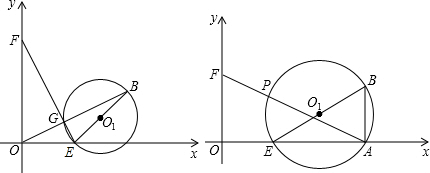
 已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.
已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.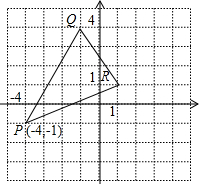 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示: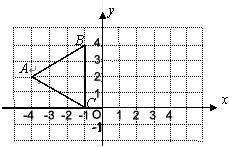 (2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
(2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )