题目内容
如图，在⊙O中，弦AB=AC=5cm，BC=8cm，则⊙O的半径等于 cm．
【答案】分析：根据等腰三角形的性质、垂径定理及勾股定理求解．
解答：
解：作AE⊥BC，垂足为E，
∵△ABC是等腰三角形，根据等腰三角形的性质，底边上的高与底边上的中线重合，
则AE是BC的中垂线，
由垂径定理的推论：弦的垂直平分线经过圆心，并且平分这条弦所对的弧知，AE的延长线过圆心，有BE=CE=
BC=4cm，
由勾股定理得AE=3cm，
连接OB，则OA=OB，OE=OA-AE=OB-AE，
由勾股定理得OB2=BE2+OE2，
设OB=x，则OE=x-3，
∴x2=42+（x-3）2，
解得x=
cm，
∴OB=
cm．
点评：本题利用了等腰三角形的性质，垂径定理，勾股定理求解．
解答：
解：作AE⊥BC，垂足为E，∵△ABC是等腰三角形，根据等腰三角形的性质，底边上的高与底边上的中线重合，
则AE是BC的中垂线，
由垂径定理的推论：弦的垂直平分线经过圆心，并且平分这条弦所对的弧知，AE的延长线过圆心，有BE=CE=
BC=4cm，由勾股定理得AE=3cm，
连接OB，则OA=OB，OE=OA-AE=OB-AE，
由勾股定理得OB2=BE2+OE2，
设OB=x，则OE=x-3，
∴x2=42+（x-3）2，
解得x=
cm，∴OB=
cm．点评：本题利用了等腰三角形的性质，垂径定理，勾股定理求解．
练习册系列答案
相关题目
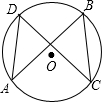已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．