题目内容
【题目】如图，在平面直角坐标系
中，把一个点
的横、纵坐标都乘以同一个实数
，然后将得到的点先向右平移
个单位，再向上平移
个单位
，得到点
（1）若
，
，
，
，则点坐标是_____；
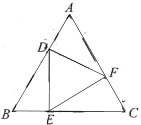
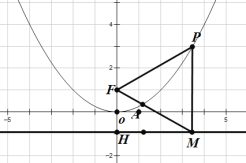
（2）对正方形
及其内部的每个点进行上述操作，得到正方形
及其内部的点，其中点
的对应点分别为
．求
；
（3）在（2）的条件下，己知正方形内部的一个点
经过上述操作后得到的对应点
与点重合，求点的坐标．
【答案】（1）
；（2）
，
，
；（3）
【解析】
（1）根据题意和平移的性质求点
坐标；
（2）由正方形的性质，结合题意列方程组求解；
（3）设点
的坐标为
，根据平移规律列方程组求解．
（1）∵
，
，
，，
∴
∴
故答案为：；
（2）根据题意得：
解得
即，，；
（3）设点的坐标为，根据题意得
解得
∴的坐标为．
练习册系列答案
相关题目
