Question

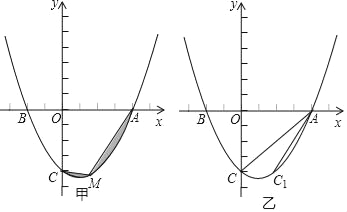
【题目】如图，已知抛物线过点A（4，0），B（﹣2，0），C（0，﹣4）．

（1）求抛物线的解析式；

（2）在图甲中，点M是抛物线AC段上的一个动点，当图中阴影部分的面积最小值时，求点M的坐标；

（3）在图乙中，点C和点C1关于抛物线的对称轴对称，点P在抛物线上，且∠PAB=∠CAC1，求点P的横坐标．

Answer 1

【答案】(1)y＝x2－x－4(2)点M的坐标为(2，－4)(3)－或－

【解析】

(1)设交点式y=a(x+2)(x-4),然后把C点坐标代入求出a即可得到抛物线解析式;
(2) 连接OM，设点M的坐标为.由题意知，当四边形OAMC面积最大时，阴影部分的面积最小．S四边形OAMC＝S△OAM＋S△OCM－(m－2)2＋12. 当m＝2时，四边形OAMC面积最大，此时阴影部分面积最小;

(3) 抛物线的对称轴为直线x＝1，点C与点C1关于抛物线的对称轴对称，所以C1(2，－4)．连接CC1，过C1作C1D⊥AC于D，则CC1＝2.先求AC＝4，CD＝C1D＝，AD＝4－＝3；设点P ，过P作PQ垂直于x轴，垂足为Q. 证△PAQ∽△C1AD，得，即，解得解得n＝－，或n＝－，或n＝4(舍去).

(1)抛物线的解析式为y＝ (x－4)(x＋2)＝x2－x－4.

(2)连接OM，设点M的坐标为.

由题意知，当四边形OAMC面积最大时，阴影部分的面积最小．

S四边形OAMC＝S△OAM＋S△OCM

＝× 4m＋× 4

＝－m2＋4m＋8＝－(m－2)2＋12.

当m＝2时，四边形OAMC面积最大，此时阴影部分面积最小，所以点M的坐标为(2，－4)．

(3)∵抛物线的对称轴为直线x＝1，点C与点C1关于抛物线的对称轴对称，所以C1(2，－4)．

连接CC1，过C1作C1D⊥AC于D，则CC1＝2.

∵OA＝OC，∠AOC＝90°，∠CDC1＝90°，

∴AC＝4，CD＝C1D＝，AD＝4－＝3，

设点P ，过P作PQ垂直于x轴，垂足为Q.

∵∠PAB＝∠CAC1，∠AQP＝∠ADC1，

∴△PAQ∽△C1AD，

∴，

即 ，化简得 ＝(8－2n)，

即3n2－6n－24＝8－2n，或3n2－6n－24＝－(8－2n)，

解得n＝－，或n＝－，或n＝4(舍去)，

∴点P的横坐标为－或－.