��Ŀ����


��3����������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���35Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������
|
�⣺��1����ͼ����ͼ�� |
 |

ĵ������ǰϦ������ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
���۵��� ��Ԫ/���� ��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ�������� ������ ������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
 ��
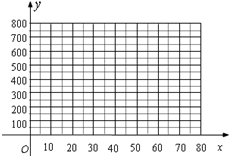
�� �ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����
�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬���� ��
�� �ĺ�����ϵ�������������ϵʽ��
�ĺ�����ϵ�������������ϵʽ����2�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�
��3����������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���35Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������

| ���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
| ÿ����������y���� | �� | 500 | 400 | 300 | 200 | 100 | �� |
��2�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ�-�ɱ��ܼۣ�
��3����������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���35Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������

ĵ������ǰϦ������ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
|
���۵��� |
�� |
20 |
30 |
40 |
50 |
60 |
�� |
|
ÿ�������� |
�� |
500 |
400 |
300 |
200 |
100 |
�� |
��1�����ϱ��� ��
�� �ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����
�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬���� ��
�� �ĺ�����ϵ�������������ϵʽ��
�ĺ�����ϵ�������������ϵʽ��
��2�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�
��3����������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���35Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������

 ��
�� ��
�� ��2012•����ĵ������ǰϦ������ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
��2012•����ĵ������ǰϦ������ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�