题目内容
a、b、c都是实数,且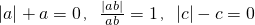 .试求
.试求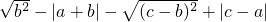 的值.
的值.
解:a、b、c都是实数,且|a|+a=0, =1,|c|-c=0,
=1,|c|-c=0,
故a≤0,b<0,c≥0,
∴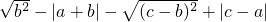
=-b+(a+b)-(c-b)+(c-a)=b.
分析:先由关系式判断a b c的符号,再根据二次根式的性质化简,去绝对值的法则得出答案.
点评:本题主要考查二次根式的化简方法与运用:a>0时, =a;a<0时,
=a;a<0时, =-a;a=0时,
=-a;a=0时, =0.
=0.
 =1,|c|-c=0,
=1,|c|-c=0,故a≤0,b<0,c≥0,
∴
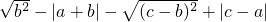
=-b+(a+b)-(c-b)+(c-a)=b.
分析:先由关系式判断a b c的符号,再根据二次根式的性质化简,去绝对值的法则得出答案.
点评:本题主要考查二次根式的化简方法与运用:a>0时,
 =a;a<0时,
=a;a<0时, =-a;a=0时,
=-a;a=0时, =0.
=0. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x、y、z都是实数,且x2+y2+z2=1,则m=xy+yz+zx( )
| A、只有最大值 | B、只有最小值 | C、既有最大值又有最小值 | D、既无最大值又无最小值 |
下列说法正确的是( )
| A、无理数都是实数 | B、实数都是无理数 | C、无限小数都是无理数 | D、带有根号的数都是无理数 |
下列说法正确的是( )
| A、有理数都是实数 | B、无限小数都是无理数 | C、带根号的数都是无理数 | D、无理数都是带根号的数 |