题目内容
若0°＜a＜90°，那么以sinα，cosα，tanα•cotα为三边的△ABC的内切圆半径r与外接圆半径R之和是
- A.
- B.
- C.2sinαcosα
- D.
A
分析：先根据三角形的三边关系判断出△ABC的形状，再根据切线长定理即可求出其内切圆的半径，由圆周角定理即可求出外接圆的半径．
解答：∵tanα•cotα=1=sinα2+cosα2，
∴△ABC是直角三角形，
如图所示，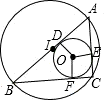
∵AD=AE，CE=CF，BD=BF，
∴内切圆的半径r=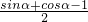
，
∵∠ACB=90°，
∴△ABC外接圆的半径R=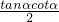
=
，
∴r+R=+=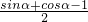
．
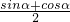故选A．
点评：本题考查的是三角形的外接圆与内切圆、同角三角函数的关系，根据题意判断出△ABC的形状是解答此题的关键．
分析：先根据三角形的三边关系判断出△ABC的形状，再根据切线长定理即可求出其内切圆的半径，由圆周角定理即可求出外接圆的半径．
解答：∵tanα•cotα=1=sinα2+cosα2，
∴△ABC是直角三角形，
如图所示，
∵AD=AE，CE=CF，BD=BF，
∴内切圆的半径r=
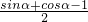，∵∠ACB=90°，
∴△ABC外接圆的半径R=
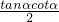=，∴r+R=
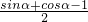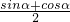+=．故选A．
点评：本题考查的是三角形的外接圆与内切圆、同角三角函数的关系，根据题意判断出△ABC的形状是解答此题的关键．
练习册系列答案
相关题目
（2013•南充模拟）如图是一个以O为对称中心的中心对称图形，若∠A=30°，∠C=90°，AC=1，则AB的长为（ ）
（2009•保定一模）某水果店购进苹果、橘子、香蕉三种水果，它们所占比例如图所示，若购进的橘子为90千克，那么，购进的苹果为
