Question

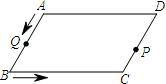如图，平行四边形ABCD中，AD=8，CD=4，∠D=60°，点P与点Q是平行四边形ABCD边上的动点，点P以每秒1个单位长度的速度，从点C运动到点D，点Q以每秒2个单位长度的速度从点A→点B→点C运动．当其中一个点到达终点时，另一个点随之停止运动．点P与点Q同时出发，设运动时间为t，△CPQ的面积为S．
（1）求S关于t的函数关系式；
（2）t为何值时，将△CPQ以它的一边为轴翻折，翻折前后的两个三角形所组成的四边形为菱形．

Answer 1

分析：（1）当0＜t≤2时，如图1，过点B作BD⊥BC，交DC的延长线于点E，根据三角形面积公式求得S关于t的函数关系式，当2＜t≤4时，如图2，CP=t，BQ=2t-4，过点P作PF⊥BC，交BC的延长线于F点，由三角形面积公式求得S关于t的函数关系式，
（2）要使翻折前后的两个三角形所组成的四边形为菱形，则△CPQ为等腰三角形，则要CQ=CP，看看t是否存在．

解答：解：（1）①当0＜t≤2时，如图1，
过点B作BE⊥DC，交DC的延长线于点E，
∴∠BCE=∠D=60°，∠CBE=30°，
∴CE=

1

2

BC=4，由勾股定理得：BE=4

3

，
∴CP=t，S=

1

2

CP•BE=

1

2

×4

3

t=2

3

t；
②当2＜t≤4时，如图2，CP=t，BQ=2t-4，CQ=8-（2t-4）=12-2t，
∵∠DCF=∠B=60°，∠F=90°，
∴∠CPF=30°，
∴CF=

1

2

CP=

1

2

t，由勾股定理得：PF=

3

2

t，
S=

1

2

CQ×PF=

1

2

×（12-2t）×

3

2

t，
即S=-

3

2

t²+3

3

t．

（2）当0＜t≤2时，△CPQ不是等腰三角形，所以不存在符合条件的菱形．
当2＜t≤4时，令CQ=CP，即t=12-2t，解得t=4．
∴当t=4时，△CPQ为等腰三角形，
即为△CPQ的一边所在直线为轴翻折，翻折前后的两个三角形组成的四边形为菱形．

点评：本题考查了四边形的综合题，解答本题多次运用解直角三角形的知识，用含t的式子表示出有关线段的长度是解答本题的关键，难度一般．