Question

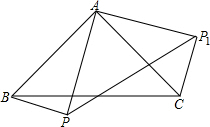（2011•红桥区一模）如图，△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后能与△ACP₁重合．若AP=3，则PP₁的长是

3

2

．

Answer 1

分析：根据题意可得△APP₁是等腰直角三角形，AP=AP₁=3，根据勾股定理，即可求得．

解答：解：∵△ABC是等腰直角三角形，
∴AB=AC，∠BAC=90°，
又∵△ABP绕点A逆时针旋转后能与△ACP₁重合，
∴AP=AP₁，∠PAP₁=90°，
∴△PAP₁是等腰直角三角形，又AP=3，
∴PP₁=3

2

．
故答案为：3

2

．

点评：本题主要考查了旋转的性质和等腰直角三角形，知道△PAP₁是等腰直角三角形是解答的关键．