题目内容
 如图,梯形ABCD,AB∥CD,∠ABC=90°,AB=9,BC=8,CD=7,M是AD的中点,从M作AD的垂线交BC于N,则BN的长是
如图,梯形ABCD,AB∥CD,∠ABC=90°,AB=9,BC=8,CD=7,M是AD的中点,从M作AD的垂线交BC于N,则BN的长是
- A..1
- B.1.5
- C.2
- D.2.5
C
分析:连接AN,DN,根据已知及线段垂直平分线的性质可得到△AMN≌△DMN从而得到AN=DN,设BN=x再根据勾股定理即可求得BN的长.
解答: 解:连接AN,DN
解:连接AN,DN
∵M是AD的中点
∴AM=DM,
∵AD⊥MN
∴∠AMN=∠DMN=90°
∵MN=MN
∴△AMN≌△DMN
∴AN=DN
假设BN=x,
在△ABN中,92+x2=AN2
在△DCN中,72+(8-x)2=DN2
∵AN=DN
∴92+x2=72+(8-x)2
x=2
故选C.
点评:本题综合考查了线段的垂直平分的性质和勾股定理的运用,作出正确的辅助线,得出AN=DN是本题解题的关键.
分析:连接AN,DN,根据已知及线段垂直平分线的性质可得到△AMN≌△DMN从而得到AN=DN,设BN=x再根据勾股定理即可求得BN的长.
解答:
 解:连接AN,DN
解:连接AN,DN∵M是AD的中点
∴AM=DM,
∵AD⊥MN
∴∠AMN=∠DMN=90°
∵MN=MN
∴△AMN≌△DMN
∴AN=DN
假设BN=x,
在△ABN中,92+x2=AN2
在△DCN中,72+(8-x)2=DN2
∵AN=DN
∴92+x2=72+(8-x)2
x=2
故选C.
点评:本题综合考查了线段的垂直平分的性质和勾股定理的运用,作出正确的辅助线,得出AN=DN是本题解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC=4cm,则EF的长等于( )
如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC=4cm,则EF的长等于( )| A、1.5cm | B、2cm | C、2.5cm | D、3cm |
 如图,梯形ABCD中,EF∥BC,AD=4,EF=5,BC=7,则DF:FC=
如图,梯形ABCD中,EF∥BC,AD=4,EF=5,BC=7,则DF:FC=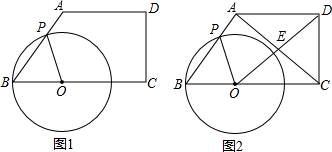
 如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为
如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为 如图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为( )
如图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为( )