题目内容
△ABC中，∠BAC=90°，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于
- A.3
- B.3
- C.2
- D.不能确定
B
分析：由AB旋转后和AC重合，得出旋转角是90°，又旋转前后长度不变，得出等腰直角三角形APP′，根据勾股定理求出即可．
解答：
解：如图：根据旋转的旋转可知：∠PAP′=∠BAC=90°，AP=AP′=3，
根据勾股定理得：PP′=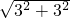
=3，
故选B．
点评：本题考查了旋转的旋转，勾股定理，等腰直角三角形等知识点的应用，根据旋转的性质得出：旋转角相等，对应点到旋转中心的距离相等，得到的△APP′是一个等腰直角三角形，是解此题的关键，再根据勾股定理求解即可．
分析：由AB旋转后和AC重合，得出旋转角是90°，又旋转前后长度不变，得出等腰直角三角形APP′，根据勾股定理求出即可．
解答：
解：如图：根据旋转的旋转可知：∠PAP′=∠BAC=90°，AP=AP′=3，根据勾股定理得：PP′=
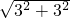=3，故选B．
点评：本题考查了旋转的旋转，勾股定理，等腰直角三角形等知识点的应用，根据旋转的性质得出：旋转角相等，对应点到旋转中心的距离相等，得到的△APP′是一个等腰直角三角形，是解此题的关键，再根据勾股定理求解即可．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
18、如图，在△ABC中，∠BAC=60°，BD、CE分别是边AC，AB上的高，BD、CE相交于点O，则∠BOC的度数是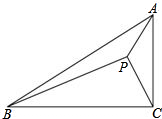
如图，△ABC中，∠BAC=60°，AB=2AC．点P在△ABC内，且PA=
如图，在△ABC中，∠BAC=90°，AB=AC=a，AD是△ABC的高，则AD的长为
93、如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BF平分∠ABC，那么△AEF是等腰三角形吗？