题目内容
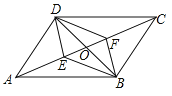
【题目】已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .

【答案】![]() .
.
【解析】
试题分析:利用全等三角形的判定AAS得出△ADF≌△ECF,进而得出FG是△DCP的中位线,得出![]() ,再利用勾股定理得出BG的长即可:
,再利用勾股定理得出BG的长即可:
如图,过点C作CP∥BG,交DE于点P.
∵BC=CE=2,∴CP是△BEG的中位线.∴P为EG的中点.
又∵AD=CE=1,AD∥CE,
∴在△ADF和△ECF中,∠AFD=∠EFC,∠ADC=∠FCE,AD=CE,
∴△ADF≌△ECF(AAS).∴CF=DF.
又CP∥FG,∴FG是△DCP的中位线.∴G为DP的中点.
∵CD=CE=2,∴DE=![]() .
.
∴![]() .
.
连接BD,
易知∠BDC=∠EDC=45°,∴∠BDE=90°.
又∵BD=![]()
∴ .
.


练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
【题目】如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.5厘米,每个铁环长4.6厘米,设铁环间处于最大限度的拉伸状态
(1)填表:
铁环个数 | 1 | 2 | 3 | 4 |
链条长(cm) | 4.6 | 8.2 | _____ | ____ |
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.17米长的链条,至少需要多少个铁环?
![]()