题目内容
某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”.小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上作些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去.小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260cm,OA、OB为圆弧的半径长为90cm(作为木杆的支架),且OA、OB关于CD对称,弧AB的长为30πcm.当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少cm?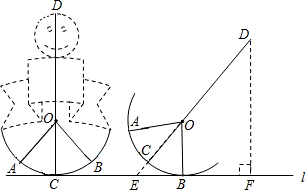
分析:根据弧长的公式先求出∠AOB=60°,从而∠BOE=∠COB=30°,再根据三角函数的知识求出木杆的顶端点D到直线l的距离DF.
解答:解:∵弧AB的长为30πcm,OA、OB为圆弧的半径长为90cm.
根据弧长的公式l=
,
得到:30π=
,
解得n=60°,即∠AOB=60°,从而∠BOE=∠COB=30°,
∵OB=90cm,∴OE=60
cm,
∴DE=170+60
cm,
∴DF=90+85
cm.
根据弧长的公式l=
| nπr |
| 180 |
得到:30π=
| nπ×90 |
| 180 |
解得n=60°,即∠AOB=60°,从而∠BOE=∠COB=30°,
∵OB=90cm,∴OE=60
| 3 |
∴DE=170+60
| 3 |
∴DF=90+85
| 3 |
点评:本题主要考查了弧长的公式l=
,及三角函数的知识,有一定的难度.
| nπr |
| 180 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



