题目内容
已知:如图所示, 为任意三角形,若将
为任意三角形,若将 绕点
绕点 顺时针旋转180° 得到
顺时针旋转180° 得到 .
.
(1)试猜想 与
与 有何关系?说明理由;
有何关系?说明理由;
(2)请给 添加一个条件,使旋转得到的四边形
添加一个条件,使旋转得到的四边形 为矩形,并说明理由.
为矩形,并说明理由.
(1)通过三角形全等求证(2)AC=BC
解析试题分析:(1)AE∥BD,AE=BD. 2分
理由:∵ 绕点C顺时针旋转180°得到
绕点C顺时针旋转180°得到 ,
,
∴ ≌
≌ ,∴AB=DE,∠ABC=∠DEC,
,∴AB=DE,∠ABC=∠DEC,
∴AB∥DE,∴四边形ABDE为平行四边形,
∴AE∥BD,AE=BD; 6分
(2)AC=BC 8分
∵AC=BC,根据旋转的性质,可得AC=BC=CE=CD,
∴AD=BE,∴四边形ABDE是矩形.
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目

 9、如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;B和D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
9、如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;B和D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
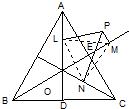 如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.
如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.