题目内容
已知矩形ABCD中，对角线AC、BD交于点0，AE⊥BD于E，OE：ED=1：3，AE=2
．BD的值为多少？
【答案】分析：由OE：ED=1：3，可知OD=2OE，根据矩形的性质：OD=OB=OA=OC，则OE=
，又因为AE⊥BD，根据勾股定理OE2+AE2=OB2，可求出OB，则BD=2OB=8．
解答：解：∵OE：ED=1：3
∴OD=2OE
∵矩形ABCD
∴OD=OB=OA=OC
∴OE=
∵AE⊥BD
∴OE2+AE2=OB2∴OB=4
∴BD=8．
点评：根据矩形的性质，配合直角三角形求解．
，又因为AE⊥BD，根据勾股定理OE2+AE2=OB2，可求出OB，则BD=2OB=8．解答：解：∵OE：ED=1：3
∴OD=2OE
∵矩形ABCD
∴OD=OB=OA=OC
∴OE=
∵AE⊥BD
∴OE2+AE2=OB2∴OB=4
∴BD=8．
点评：根据矩形的性质，配合直角三角形求解．
练习册系列答案
名校课堂系列答案
相关题目
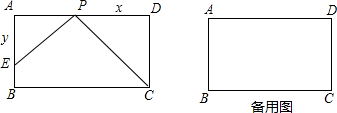
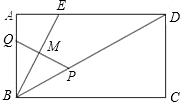
，点Q从点B以每秒1个单位沿BA方向向点A运动，设运动时间为t秒，△BPQ的面积为S．
如图，已知矩形ABCD中，BC=6，AB=8，延长AD到点E，使AE=15，连接BE交AC于点P．
如图：已知矩形ABCD中，CE∥DF．