题目内容
如图，“五•一”期间在某商贸大厦上从点A到点B悬挂了一条宣传条幅，小明和小雯的家正好住在商贸大厦对面的家属楼上，小明在四楼D点测得条幅端点A的仰角为30°，测得条幅端点B的俯角为45°；小雯在三楼仰角为45°，测得条幅端点B的俯角为30°．若设楼层高度CD为3米，请你根据小明和小雯测得的数据求出条幅AB的长．（结果精确到个位，参考数据
| 3 |
分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形△AGD、△AHC，应利用矩形性质构造方程关系式，进而可解即可求出答案．
解答：
解：分别过点D、C作DG⊥AB于G点，CH⊥AB于H点．
∵DG⊥AE，CH⊥AE，
∴DG∥CH，
∵AE∥DF，
∴四边形DGHC是矩形．
设AG=x，则BH=x，
在Rt△AGD中，DG=
x，
在Rt△AHC中，
∵∠ACH=45°，
∴AH=CH=
x，
所以AH-AG=DC=3，即
x-x=3，
所以x=
，
AB=AG+GH+HB=
+3≈11m，
答：条幅AB的长是11m．
解：分别过点D、C作DG⊥AB于G点，CH⊥AB于H点．∵DG⊥AE，CH⊥AE，
∴DG∥CH，
∵AE∥DF，
∴四边形DGHC是矩形．
设AG=x，则BH=x，
在Rt△AGD中，DG=
| 3 |
在Rt△AHC中，
∵∠ACH=45°，
∴AH=CH=
| 3 |
所以AH-AG=DC=3，即
| 3 |
所以x=
| 3 | ||
|
AB=AG+GH+HB=
| 2×3 | ||
|
答：条幅AB的长是11m．
点评：命题立意：考查利用解直角三角形知识解决实际问题的能力．要求学生应用数学知识解决问题，在正确分析题意的基础上建立数学模型，把实际问题转化为数学问题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
元的购书券，凭购书券可以在书城继续购书，如果读者不愿意转转盘，那么可以直接获得10元的购书券．
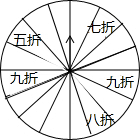世博会期间，某高级酒店为了吸引顾客，设立了一个可以自由转动的转盘，如图所示，并规定：顾客消费100元以上（不包括100元），就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准九折、八折、七折、五折区域顾客就可以获得相应的打折优惠（转盘等分成16份，指针停在每个区域的机会相等）．
