题目内容
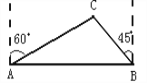
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点于
轴交点于![]() ,且
,且![]() ,
,![]() °,以
°,以![]() 为边长作等边三角形
为边长作等边三角形![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为边长作等边三角行
为边长作等边三角行![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]()
![]() 为边长坐等三角形
为边长坐等三角形![]() ,…,则点
,…,则点![]() 的横坐标是___________.
的横坐标是___________.
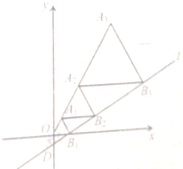
【答案】![]()
【解析】过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为![]() ,,A2的横坐标为
,,A2的横坐标为![]() , A3的横坐标为
, A3的横坐标为![]() ,进而得到An的横坐标为
,进而得到An的横坐标为![]() ,据此可得点A10的横坐标.
,据此可得点A10的横坐标.
解:如图所示,过A1作A1A⊥OB1于A,则OA=![]() OB1=
OB1=![]() ,
,

即A1的横坐标为![]() =
=![]() ,
,
∵![]() °,
°,
∴∠OB1D=30°,
∵A1B2//x轴,
∴∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=![]() A1B2=1,
A1B2=1,
即A2的横坐标为![]() +1=
+1=![]() ,
,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=![]() A2B3=2,
A2B3=2,
即A3的横坐标为![]() +1+2=
+1+2=![]() ,
,
同理可得,A4的横坐标为![]() +1+2+4=
+1+2+4=![]() ,
,
由此可得,An的横坐标为![]() ,
,
∴点A10的横坐标是![]() ,
,
故答案为:![]() .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
【题目】某数学兴趣小组根据学习函数的经验,对函数![]() 的图象与性质进行了探究,下面是该小组的探究过程,请补充完整:
的图象与性质进行了探究,下面是该小组的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是________:
的取值范围是________:
(2)列表,找出![]() 与
与![]() 的几组对应值:
的几组对应值:
|
| -1 | 0 | 1 | 2 | 3 |
|
|
|
| 1 | 0 | 1 | 2 |
|
其中,![]() _______:
_______:
(3)在平面直角坐标系![]() 中,描出以上表中对应值为坐标的点,并画出该函数的图像.
中,描出以上表中对应值为坐标的点,并画出该函数的图像.