题目内容
如图,直线 交x轴于A点,交y轴于B点,抛物线
交x轴于A点,交y轴于B点,抛物线 经过点A、B,交x轴于另一点C,顶点为D.
经过点A、B,交x轴于另一点C,顶点为D.
(1)求抛物线的函数表达式;
(2)求点C、D两点的坐标;
(3)求△ABD的面积;
(1) ;(2)c(1,0),D(-1,4);(3)3.
;(2)c(1,0),D(-1,4);(3)3.
解析试题分析:(1)求出A、B的坐标,代入抛物线的解析式即可;
(2)令 ,即可求出抛物线与
,即可求出抛物线与 轴的两个交点,把抛物线化成顶点式即可得到顶点坐标;
轴的两个交点,把抛物线化成顶点式即可得到顶点坐标;
(3)设对称轴与x轴交于点E,则△ABD的面积=△ADE的面积+梯形DEOB的面积-△AOB的面积.
试题解析:(1)在 中,令
中,令 ,得
,得 ,∴B(0,3);令
,∴B(0,3);令 ,得:
,得: ,∴A(-3,0),∴
,∴A(-3,0),∴ ,解得:
,解得: ,∴抛物线的解析式为:
,∴抛物线的解析式为: ;
;
(2)在 中,令
中,令 ,得:
,得: ,解得:
,解得: ,
, ,∴C(1,0),∵
,∴C(1,0),∵ ∴顶点D的坐标为(-1,4);
∴顶点D的坐标为(-1,4);
(3)设抛物线对称轴与 轴相交于点E,∵A(-3,0),B(0,3),D (-1,4),∴AE=2,DE=4,OE=1,OB=3,
轴相交于点E,∵A(-3,0),B(0,3),D (-1,4),∴AE=2,DE=4,OE=1,OB=3,
∴
= ×AE×DE+
×AE×DE+ ×(DE+OB) ×OE-
×(DE+OB) ×OE- AO×OB=
AO×OB= .
.
考点:二次函数综合题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目

 ,
, ,
, .
.


 .
. ).
).
 )是否在该二次函数图象上;并指出当
)是否在该二次函数图象上;并指出当 取何值时,
取何值时,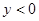 ?
? 与直线
与直线 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.