题目内容
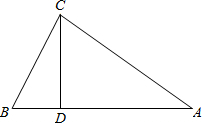 已知:如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,CD⊥AB于D.
已知:如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,CD⊥AB于D.
①求AC的长;②求S△ABC;③求CD的长.
解:①∵在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
∴根据勾股定理知,AC= =8cm;
=8cm;
②由①知,AC=8cm.则S△ABC= AC•BC=
AC•BC= ×8×6=24(cm2);
×8×6=24(cm2);
③由①知,AC=8cm;由②知S△ABC=24cm2;
则 AB•CD=
AB•CD= ×10•CD=24,
×10•CD=24,
解得,CD=4.8(cm).
分析:①在直角三角形ABC中根据勾股定理可以求得AC的长度;
②根据直角三角形的面积公式求得三角形ABC的面积;
③根据三角形的面积公式知 CD•AB=
CD•AB= BC•AC,据此可以求得CD的长度.
BC•AC,据此可以求得CD的长度.
点评:本题考查了勾股定理、直角三角形的面积公式.解题时充分利用了直角三角形的面积的求法.
∴根据勾股定理知,AC=
 =8cm;
=8cm;②由①知,AC=8cm.则S△ABC=
 AC•BC=
AC•BC= ×8×6=24(cm2);
×8×6=24(cm2);③由①知,AC=8cm;由②知S△ABC=24cm2;
则
 AB•CD=
AB•CD= ×10•CD=24,
×10•CD=24,解得,CD=4.8(cm).
分析:①在直角三角形ABC中根据勾股定理可以求得AC的长度;
②根据直角三角形的面积公式求得三角形ABC的面积;
③根据三角形的面积公式知
 CD•AB=
CD•AB= BC•AC,据此可以求得CD的长度.
BC•AC,据此可以求得CD的长度.点评:本题考查了勾股定理、直角三角形的面积公式.解题时充分利用了直角三角形的面积的求法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,