Question

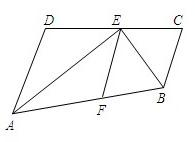
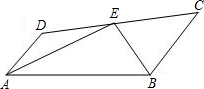
如图：E在线段CD上，EA、EB分别平分∠DAB和∠CBA，∠AEB=90°，设AD=x，BC=y，且（x-3）²+|y-4|=0
（1）求AD和BC的长；
（2）你认为AD和BC还有什么关系？并验证你的结论．

Answer 1

解：（1）∵（x-3）²+|y-4|=0，
∴x-3=0，y-4=0，
解得：x=3，y=4，
∴AD=3，BC=4；

（2）AD∥BC．
理由：∵EA、EB分别平分∠DAB和∠CBA，
∴∠DAE=∠EAB，∠CBE=∠EBA，
∵∠AEB=90°，∴∠EAB+∠EBA=90°，
∴∠DAE+∠EBC=90°，
∴∠EAB+∠EBA+∠DAE+∠EBC=90°+90°=180°，
∴AD∥BC．
分析：（1）根据绝对值和完全平方公式的性质得出x，y的值即可得出答案；
（2）根据已知得出∠EAB+∠EBA+∠DAE+∠EBC=90°+90°=180°，再由平行线的判定得出即可．
点评：此题主要考查了平行线的判定和绝对值的性质等知识，根据已知得出∠DAE+∠EBC=90°是解题关键．