题目内容
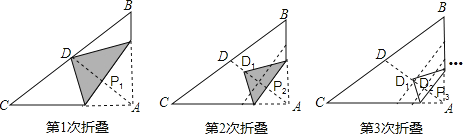
【题目】如图，直角三角形纸片ABC中，AB＝3，AC＝4．D为斜边BC的中点，第1次将纸片折叠，使点A与点D重合，折痕与AD交于点P1；设P1D的中点为D1，第2次将纸片折叠，使点A与点D1重合，折痕与AD交于点P2；设P2D1的中点为D2，第3次将纸片折叠，使点A与点D2重合，折痕与AD交于点P3；设Pn﹣1Dn﹣2的中点为Dn﹣1，第n次将纸片折叠，使点A与点Dn﹣1重合，折痕与AD交于点Pn（n＞2），则AP2019的长为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
先写出AD、AD1、AD2、AD3的长度，然后可发现规律推出ADn的表达式，继而根据APn＝
ADn即可得出APn的表达式，也可得出AP2019的长．
解：由题意得，AD＝
BC＝
，
AD1＝AD﹣DD1＝
，
AD2＝
，
AD3＝
，…，
ADn＝
，
又∵AP1＝AD1，AP2＝AD2…，
∴APn＝ADn，
∴AP3＝
，APn＝
，
故AP2019的长为：
．
故选：C．
练习册系列答案
相关题目
【题目】某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间，经市场调查表明，该宾馆每间标准房的价格在170~240元之间（含170元，240元）浮动时，每天入住的房间数
（间）与每间标准房的价格
（元）的数据如下表：
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
（1）根据所给数据在坐标系中描出相应的点，并画出图象.
（2）求关于的函数表达式、并写出自变量的取值范围.
（3）设客房的日营业额为
（元）.若不考虑其他因素，问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元？
