题目内容
已知：△ABC中，AD为中线，∠BAD=60°，AB=10，BC=4
，求AC的长．
| 19 |
分别过B、C作BF⊥AD于F，CE⊥AD于E，
在Rt△AFB中，∠BAF=60°，AB=10，
sin∠BAF=
，
∴BF=ABsin∠BAF=5
．
cos∠BAF=
，
∴AF=ABcos∠BAF=5．
BC=4
，AD为中线，
∴BD=DC=2
．
在Rt△BFD中，DF=
=
=1，
∵D为BC中点，∴BD=CD，
又CE⊥AD，BF⊥AD，
∴∠ADC=∠BDF．
∴△BDF≌△CDE（AAS）．
∴DE=DF=1．
∴AE=5-2=3，CE=BF=5
．
在Rt△AEC中，AC=
=
=2
，
又若△ABC'时，AE'=5+2=7，C'E'=5
，
在Rt△AE'C'中，A'C'=
=2
，
∴AC的长为2
或2
．
在Rt△AFB中，∠BAF=60°，AB=10，
sin∠BAF=
| BF |
| AB |
∴BF=ABsin∠BAF=5
| 3 |
cos∠BAF=
| AF |
| AB |
∴AF=ABcos∠BAF=5．
BC=4
| 19 |
∴BD=DC=2
| 19 |
在Rt△BFD中，DF=
| BD2-BF2 |
(2
|
∵D为BC中点，∴BD=CD，
又CE⊥AD，BF⊥AD，
∴∠ADC=∠BDF．
∴△BDF≌△CDE（AAS）．
∴DE=DF=1．
∴AE=5-2=3，CE=BF=5
| 3 |
在Rt△AEC中，AC=
| AE2+CE2 |
32+(5
|
| 21 |
又若△ABC'时，AE'=5+2=7，C'E'=5
| 3 |
在Rt△AE'C'中，A'C'=
| AE′2+C′E′2 |
| 31 |
∴AC的长为2
| 31 |
| 21 |
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
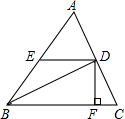BC，交AB于E，过D作DF⊥BC，垂足为F，连接BD，设CD=x．
