题目内容
已知:△ABC中,BC=3,AC=4,AB=5.若将△ABC沿最长边AB翻折,使得到的△ABC′与△ABC在同一个平面内,则CC′等于
- A.

- B.

- C.

- D.

D
分析:根据勾股定理的逆定理,知△ABC是直角三角形;根据轴对称的性质,得AB垂直平分CC′;根据直角三角形斜边上的高等于两条直角边的乘积除以斜边即可求解.
解答: 解:∵BC=3,AC=4,AB=5,
解:∵BC=3,AC=4,AB=5,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
根据折叠的性质,得AB垂直平分CC′.
∴CD= =
= .
.
∴CC′=2CD= .
.
故选D.
点评:此题综合运用了勾股定理的逆定理、直角三角形的斜边上的高的求法以及轴对称的性质.
直角三角形斜边上的高等于两条直角边的乘积除以斜边.
分析:根据勾股定理的逆定理,知△ABC是直角三角形;根据轴对称的性质,得AB垂直平分CC′;根据直角三角形斜边上的高等于两条直角边的乘积除以斜边即可求解.
解答:
 解:∵BC=3,AC=4,AB=5,
解:∵BC=3,AC=4,AB=5,∴BC2+AC2=AB2,
∴△ABC是直角三角形.
根据折叠的性质,得AB垂直平分CC′.
∴CD=
 =
= .
.∴CC′=2CD=
 .
.故选D.
点评:此题综合运用了勾股定理的逆定理、直角三角形的斜边上的高的求法以及轴对称的性质.
直角三角形斜边上的高等于两条直角边的乘积除以斜边.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
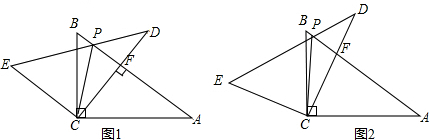
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.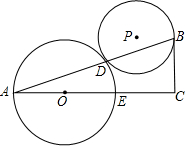 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,