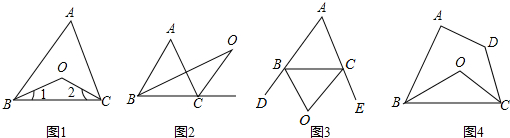
题目内容
在△ABC中，I是∠ABC、∠ACB的角平分线的交点，∠BIC=100°，则∠A的度数是
- A.20°
- B.50°
- C.65°
- D.80°
A
分析：根据角平分线的定义和三角形内角和等于180°，先求出∠ABC与∠ACB的一半的度数之和，然后求出∠ABC、∠ACB的度数之和，再根据三角形内角和等于180°即可求出∠A的度数．
解答：∵∠BIC=100°，
∴
（∠ABC+∠ACB）=180°-100°=80°，
∴∠ABC+∠ACB=80°×2=160°，
在△ABC中，∠A=180°-∠ABC-∠ACB=180°-160°=20°．
故选A．
点评：本题主要利用三角形的内角和定理求解，熟练掌握定理是解题的关键．
分析：根据角平分线的定义和三角形内角和等于180°，先求出∠ABC与∠ACB的一半的度数之和，然后求出∠ABC、∠ACB的度数之和，再根据三角形内角和等于180°即可求出∠A的度数．
解答：∵∠BIC=100°，
∴
（∠ABC+∠ACB）=180°-100°=80°，∴∠ABC+∠ACB=80°×2=160°，
在△ABC中，∠A=180°-∠ABC-∠ACB=180°-160°=20°．
故选A．
点评：本题主要利用三角形的内角和定理求解，熟练掌握定理是解题的关键．
练习册系列答案
相关题目
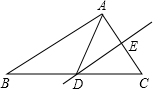如图所示，在△ABC中，DE是AC的中垂线，AE=3cm，△ABD得周长为13cm，则△ABC的周长是
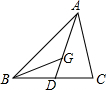如图，在△ABC中，AD是中线，G是重心，
如图在△ABC中，AD是BC边上的高，BE平分∠ABD，交AD于E．已知∠BED=60°，∠BAC=50°，则∠C=（ ）