题目内容
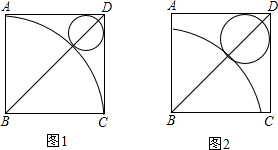
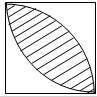已知正方形边长为a，分别以正方形相对的两个顶点为圆心，以a为半径画弧（1）用多项式表示图中的阴影部分的面积；
（2）当a=2时，阴影部分的面积是多少？
考点：列代数式,代数式求值
专题：计算题
分析：（1）图中的阴影部分的面积等于半径为a，圆心角为90°的两个扇形面积减去正方形的面积，然后根据扇形面积公式和正方形面积公式表示即可；
（2）把a=2代入（1）中的代数式中计算即可．
（2）把a=2代入（1）中的代数式中计算即可．
解答：解：（1）图中的阴影部分的面积=2•
-a2，
=（
-1）a2；
（2）当a=2时，图中的阴影部分的面积=（
-1）•4=2π-4．
| 90•π•a2 |
| 360 |
=（
| π |
| 2 |
（2）当a=2时，图中的阴影部分的面积=（
| π |
| 2 |
点评：本题考查了列代数式：把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式．也考查了利用面积的和差求不规则图形的面积．
练习册系列答案
相关题目
已知m＞2，点（m-2，y1），（m，y2）（m+2，y3）都在函数y=x2的图象上，则（ ）
| A、y1＜y2＜y3 |
| B、y1＜y3＜y2 |
| C、y3＜y2＜y1 |
| D、y2＜y1＜y3 |
已知线段OA⊥OB，C为OB上中点，D为AO上一点，连AC、BD交于P点．当OA=OB，