题目内容

【题目】如图，过半径为6的圆O上一点A作圆O的切线l，P为圆O的一个动点，作PH⊥l于点H，连接PA．如果PA=x，AH=y，那么下列图象中，能大致表示y与x的函数关系的是（ ）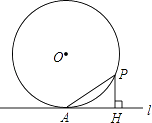

A.
B.
C.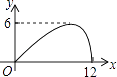
D.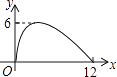

【答案】C
【解析】解：如图，当PH与圆O相切时，

∵四边形OAHP是正方形，

∴AH=6，PA=6 ，

当点P在圆O上运动时，y与x之间的关系既不是一次函数也不是二次函数，并且在x=6 时，函数取得最大值6，

因为6＜6 ＜12，

所以答案是：C．

【考点精析】掌握函数的图象和切线的性质定理是解答本题的根本，需要知道函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．

练习册系列答案
相关题目

【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=∠ADC=90°，对角线AC，BD交于点O，DE平分∠ADC交BC于点E，连接OE．

（1）求证：四边形ABCD是矩形；

（2）若AB=2，求△OEC的面积．

【题目】将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.

（1）求证：四边形ABCD是菱形；

（2）如果两张矩形纸片的长都是8，宽都是2．那么△DCB的面积是否存在最大值或最小值？如果存在，请求出来；如果不存在，请简要说明理由.

【题目】某市三景区是人们节假日游玩的热点景区，某学校对九（1）班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查，调查分四个类别，A：三个景区；B：游两个景区；C：游一个景区；D：不到这三个景区游玩，现根据调查结果绘制了不完全的条形统计图和扇形统计图如下：

请结合图中信息解答下列问题：
（1）九（1）班现有学生人，在扇形统计图中表示“B类别”的扇形的圆心角的度数为；
（2）请将条形统计图补充完整；
（3）若该校九年级有1000名学生，求计划“五一”小长假随父母到这三个景区游玩的学生多少名？

【题目】在四边形ABCD中，AB=AD，BC=CD．
（1）如图1，请连接AC，BD，求证：AC垂直平分BD；

（2）如图2，若∠BCD=60°，∠ABC=90°，E，F分别为边BC，CD上的动点，且∠EAF=60°，AE，AF分别与BD交于G，H，求证：△AGH∽△AFE；

（3）如图3，在（2）的条件下，若 EF⊥CD，直接写出 的值．

【题目】如图1，在平面直角坐标系中，点A的坐标为（-4，4），点B的坐标为（0，2）．

（1）求直线AB的解析式；

（2）以点A为直角顶点作∠CAD=90°，射线AC交x轴的负半轴于点C，射线AD交y轴的负半轴于点D．当∠CAD绕着点A旋转时，OC-OD的值是否发生变化？若不变，求出它的值；若变化，求出它的变化范围；

（3）如图2，点M（-4，0）和N（2，0）是x轴上的两个点，点P是直线AB上一点．当△PMN是直角三角形时，请求出满足条件的所有点P的坐标．

【题目】如图，直线AB、CD相交于点O，OE是∠AOD的平分线，若∠AOC＝60°，OF⊥OE．

（1）判断OF把∠AOC所分成的两个角的大小关系并证明你的结论；

（2）求∠BOE的度数．

【题目】某商品交易会上，一商人将每件进价为5元的纪念品，按每件9元出售，每天可售出32件．他想采用提高售价的办法来增加利润，经试验，发现这种纪念品每件提价2元，每天的销售量会减少8件．
（1）当售价定为多少元时，每天的利润为140元？
（2）写出每天所得的利润y（元）与售价x（元/件）之间的函数关系式，每件售价定为多少元，才能使一天所得的利润最大？最大利润是多少元？（利润=（售价﹣进价）×售出件数）

【题目】如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．

（1）判断直线CD和⊙O的位置关系，并说明理由．
（2）过点B作⊙O的切线BE交直线CD于点E，若AC=2，⊙O的半径是3，求∠BEC的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网