题目内容
已知:如图,直角梯形ABCD中AD∥BC,∠A=90°,CD=CB=2AD.点Q是AB边中点,点P在CD边上运动,以点P为直角顶点作直角∠MPN,∠MPN的两边分别与AB边、CB边交于点M、N.
(1)若点P与点D重合,点M在线段AQ上,如图(1).求证:
MQ-CN=
BC.
(2)若点P是CD中点,点M在线段BQ上,如图(2).线段MQ、CN、BC的数量关系是:
MQ+CN=
BC
MQ+CN=
BC,并证明你的猜想.

(1)若点P与点D重合,点M在线段AQ上,如图(1).求证:
| 3 |
| 1 |
| 4 |
(2)若点P是CD中点,点M在线段BQ上,如图(2).线段MQ、CN、BC的数量关系是:
| ||
| 3 |
| 1 |
| 4 |
| ||
| 3 |
| 1 |
| 4 |

分析:(1)过点D作DE⊥BC于E,可得四边形ABED是矩形,根据矩形的对边相等可得BE=AD,设AD=x,表示出CD=CB=2x,再求出CE=BE,再利用勾股定理列式求出DE,再根据等角的余角相等求出∠DAM=∠EDN,证明Rt△ADM和Rt△EDN相似,根据相似三角形对应边成比例列出比例式,然后代入进行计算求出AM、EN的关系,再表示出MQ、CN并代入
MQ-CN整理即可得解;
(2)连接PQ,过点D作DE⊥BC于E,过点P作PF⊥BC于F,设AD=x,则CD=CB=2x,根据梯形的中位线平行于底边并且等于两底和的一半求出PQ∥AD,PQ=
(AD+CB),再根据(1)得到DE的长,根据三角形的中位线平行于第三边并且等于第三边的一半可得PF∥DE,PF=
DE,根据同角的余角相等求出∠QPM=∠FPN,然后求出△PQM和△PFN相似,利用相似三角形对应边成比例列式求出MQ和FN的关系,再表示出CN,整理即可得解.
| 3 |
(2)连接PQ,过点D作DE⊥BC于E,过点P作PF⊥BC于F,设AD=x,则CD=CB=2x,根据梯形的中位线平行于底边并且等于两底和的一半求出PQ∥AD,PQ=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)如图1,过点D作DE⊥BC于E,
∵AD∥BC,∠A=90°,
∴四边形ABED是矩形,
∴BE=AD,
设AD=x,则CD=CB=2x,
∵CD=CB=2AD=2x,
∴CE=BE=2x-x=x,
∴在Rt△CDE中,根据勾股定理得,DE=
=
=
x,
∵∠MPN是直角,
∴∠MDE+∠EDN=90°,
又∵∠ADM+∠MDE=90°,
∴∠DAM=∠EDN,
∴Rt△ADM∽Rt△EDN,
∴
=
,
即
=
,
∴EN=
AM,
∵点Q是AB边中点,
∴AQ=
AB=
DE=
x,
∴MQ=AQ-AM=
x-AM,
∴
MQ-CN=
(
x-AM)-(x-
AM)=
x-
AM-x+
AM=
x,
∵CB=2x,
∴
x=
BC,
∴
MQ-CN=
BC;
(2)如图2,连接PQ,过点D作DE⊥BC于E,过点P作PF⊥BC于F,设AD=x,则CD=CB=2x,
∵点P是CD中点,点Q是AB的中点,
∴PQ∥AD,PQ=
(AD+CB)=
(x+2x)=
x,
同(1)可求,DE=
x,
∵点P是CD中点,
∴PF∥DE,PF=
DE=
x,CF=
CE=
x,
又∵∠QPM+∠MPN=∠FPN+∠MPN,
∴∠QPM=∠FPN,
∴△PQM∽△PFN,
∴
=
,
即
=
,
∴FN=
MQ,
∴CN=CE-FN=
x-
MQ,
∵CB=2x,
∴
x=
BC,
∴
MQ+CN=
BC.
故答案为:
MQ+CN=
BC.
∵AD∥BC,∠A=90°,
∴四边形ABED是矩形,
∴BE=AD,
设AD=x,则CD=CB=2x,
∵CD=CB=2AD=2x,
∴CE=BE=2x-x=x,
∴在Rt△CDE中,根据勾股定理得,DE=
| CD2-CE2 |
| (2x)2-x2 |
| 3 |
∵∠MPN是直角,
∴∠MDE+∠EDN=90°,
又∵∠ADM+∠MDE=90°,
∴∠DAM=∠EDN,
∴Rt△ADM∽Rt△EDN,

∴
| AD |
| DE |
| AM |
| EN |
即
| x | ||
|
| AM |
| EN |
∴EN=
| 3 |
∵点Q是AB边中点,
∴AQ=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴MQ=AQ-AM=
| ||
| 2 |
∴
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
∵CB=2x,
∴
| 1 |
| 2 |
| 1 |
| 4 |
∴
| 3 |
| 1 |
| 4 |
(2)如图2,连接PQ,过点D作DE⊥BC于E,过点P作PF⊥BC于F,设AD=x,则CD=CB=2x,
∵点P是CD中点,点Q是AB的中点,
∴PQ∥AD,PQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
同(1)可求,DE=
| 3 |
∵点P是CD中点,
∴PF∥DE,PF=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
又∵∠QPM+∠MPN=∠FPN+∠MPN,
∴∠QPM=∠FPN,
∴△PQM∽△PFN,
∴
| PQ |
| PF |
| MQ |
| FN |
即
| ||||
|
| MQ |
| FN |
∴FN=
| ||
| 3 |
∴CN=CE-FN=
| 1 |
| 2 |
| ||
| 3 |
∵CB=2x,
∴
| 1 |
| 2 |
| 1 |
| 4 |
∴
| ||
| 3 |
| 1 |
| 4 |
故答案为:
| ||
| 3 |
| 1 |
| 4 |
点评:本题是相似形综合题,主要利用了矩形的判定,同角的余角相等的性质,相似三角形的判定与性质,梯形的中位线平行于底边并且等于两底和的一半,三角形的中位线平行于第三边并且等于第三边的一半的性质,综合性较强,但难度不大,作出辅助线构造出直角三角形与相似三角形是解题的关键.

练习册系列答案
相关题目
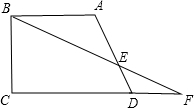 已知:如图,直角梯形ABCD中,∠BCD=90°,∠CDA=60°,AB=AD,AB=4,DF=2,求BF的长.
已知:如图,直角梯形ABCD中,∠BCD=90°,∠CDA=60°,AB=AD,AB=4,DF=2,求BF的长.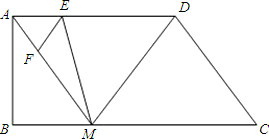 、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.
、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.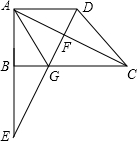
 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.