题目内容
 如图,抛物线y=x2+1与双曲线y=
如图,抛物线y=x2+1与双曲线y= 的交点A的横坐标是2,则关于x的不等式-
的交点A的横坐标是2,则关于x的不等式- +x2+1>0的解集是
+x2+1>0的解集是
- A.x>2
- B.x<0 或x>2
- C.0<x<2
- D.-2<x<0
B
分析:由- +x2+1>0,即可得x2+1>
+x2+1>0,即可得x2+1> ,又由抛物线y=x2+1与双曲线y=
,又由抛物线y=x2+1与双曲线y= 的交点A的横坐标是2,观察图象可得当x<0 或x>2时,x2+1>
的交点A的横坐标是2,观察图象可得当x<0 或x>2时,x2+1> ,继而求得关于x的不等式-
,继而求得关于x的不等式- +x2+1>0的解集.
+x2+1>0的解集.
解答:∵- +x2+1>0,
+x2+1>0,
∴x2+1> ,
,
∵抛物线y=x2+1与双曲线y= 的交点A的横坐标是2,
的交点A的横坐标是2,
结合图象可得:当x<0 或x>2时,x2+1> ,
,
即关于x的不等式- +x2+1>0的解集是:x<0 或x>2.
+x2+1>0的解集是:x<0 或x>2.
故选B.
点评:此题考查了二次函数与不等式的关系.此题难度适中,注意掌握图象与不等式的关系是解此题的关键,注意数形结合思想的应用.
分析:由-
 +x2+1>0,即可得x2+1>
+x2+1>0,即可得x2+1> ,又由抛物线y=x2+1与双曲线y=
,又由抛物线y=x2+1与双曲线y= 的交点A的横坐标是2,观察图象可得当x<0 或x>2时,x2+1>
的交点A的横坐标是2,观察图象可得当x<0 或x>2时,x2+1> ,继而求得关于x的不等式-
,继而求得关于x的不等式- +x2+1>0的解集.
+x2+1>0的解集.解答:∵-
 +x2+1>0,
+x2+1>0,∴x2+1>
 ,
,∵抛物线y=x2+1与双曲线y=
 的交点A的横坐标是2,
的交点A的横坐标是2,结合图象可得:当x<0 或x>2时,x2+1>
 ,
,即关于x的不等式-
 +x2+1>0的解集是:x<0 或x>2.
+x2+1>0的解集是:x<0 或x>2.故选B.
点评:此题考查了二次函数与不等式的关系.此题难度适中,注意掌握图象与不等式的关系是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
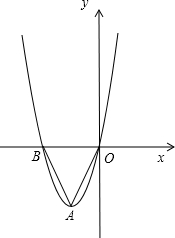 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.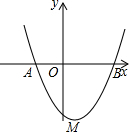 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.