题目内容
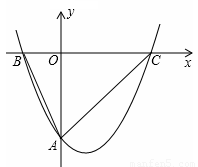
 如图,经过原点的抛物线y1=x2+2x与x轴交于点A,将它平移得到抛物线y2=(x-2)2+1.有以下结论:
如图,经过原点的抛物线y1=x2+2x与x轴交于点A,将它平移得到抛物线y2=(x-2)2+1.有以下结论:
①y2是由y1先向上平移1个单位,再向右平移2个单位得到的;
②无论x取何值,y2≥1;
③当x=0时,y2-y1=5;
④当y1<0时,-2<x<0.
其中正确的结论是
- A.①②③
- B.②③④
- C.①③④
- D.①②④
B
分析:利用二次函数图象以及平移的性质分别求出即可.
解答:∵y1=x2+2x=(x+1)2-1,y2=(x-2)2+1,
∴①y2是由y1先向上平移2个单位,再向右平移3个单位得到的,故此选项错误;
∵y2=(x-2)2+1,
∴②无论x取何值,y2≥1,故此选项正确;
③当x=0时,y2-y1=(0-2)2+1-[(0+1)2-1]=5;故此选项正确;
④∵y1=x2+2x=x(x+2),
∴图象与x轴的交点坐标为:(0,0),(-2,0),
当y1<0时,-2<x<0,故此选项正确.
故选:B.
点评:此题主要考查了二次函数的平移变换以及二次函数的增减性等知识,利用数形结合得出是解题关键.
分析:利用二次函数图象以及平移的性质分别求出即可.
解答:∵y1=x2+2x=(x+1)2-1,y2=(x-2)2+1,
∴①y2是由y1先向上平移2个单位,再向右平移3个单位得到的,故此选项错误;
∵y2=(x-2)2+1,
∴②无论x取何值,y2≥1,故此选项正确;
③当x=0时,y2-y1=(0-2)2+1-[(0+1)2-1]=5;故此选项正确;
④∵y1=x2+2x=x(x+2),
∴图象与x轴的交点坐标为:(0,0),(-2,0),
当y1<0时,-2<x<0,故此选项正确.
故选:B.
点评:此题主要考查了二次函数的平移变换以及二次函数的增减性等知识,利用数形结合得出是解题关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为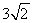
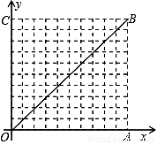
 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )